题目内容
15．某文具店销售甲、乙两种圆规，当销售5只甲种、1只乙种圆规，可获利润25元，销售6只甲种、3只乙种圆规，可获利润39元．（1）问该文具店销售甲、乙两种圆规，每只的利润分别是多少元？
（2）在（1）中，文具店共销售甲、乙两种圆规50只，其中甲种圆规为a只，求文具店所获得利润P与a的函数关系式，并求当a≥30时P的最大值．
分析 （1）根据题意可以列出相应的方程组，然后解方程组即可解答本题；
（2）根据题意可以列出文具店所获利p与a的函数关系式，然后根据当a≥30，可以求得p的最大值．
解答 解：（1）设文具店销售甲、乙两种圆规，每只的利润分别是x元、y元，
$\left\{\begin{array}{l}{5x+y=25}\\{6x+3y=39}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$，
即文具店销售甲、乙两种圆规，每只的利润分别是4元、5元；
（2）由题意可得，
p=4a+5（50-a）=4a+250-5a=250-a，
∵a≥30，
∴当a=30时，p取得最大值，此时，p=250-30=220，
即文具店所获利p与a的函数关系式是p=250-a，当a≥30时p的最大值是220．
点评 本题考查一次函数的应用，二元一次方程组的应用，解题的关键是明确题意，列出相应的关系式，找出所求问题需要的条件．
练习册系列答案
阅读快车系列答案
相关题目
3．
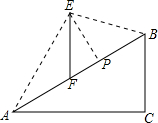如图，在坡度i=1：$\sqrt{3}$的斜坡AB上立有一电线杆EF，工程师在点A处测得E的仰角为60°，沿斜坡前进20米到达B，此时测得点E的仰角为15°，现要在斜坡AB上找一点P，在P处安装一根拉绳PE来固定电线杆，以使EF保持竖直，为使拉绳PE最短，则FP的长度约为（ ）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
如图，在坡度i=1：$\sqrt{3}$的斜坡AB上立有一电线杆EF，工程师在点A处测得E的仰角为60°，沿斜坡前进20米到达B，此时测得点E的仰角为15°，现要在斜坡AB上找一点P，在P处安装一根拉绳PE来固定电线杆，以使EF保持竖直，为使拉绳PE最短，则FP的长度约为（ ）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）| A． | 3.7米 | B． | 3.9米 | C． | 4.2米 | D． | 5.7米 |
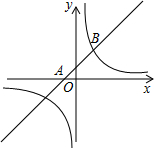如图，一次函数y=mx+1的图象经过点A（-1，0），且与反比例函数y=$\frac{k}{x}$（k≠0）交于点B（n，2）．