题目内容
7.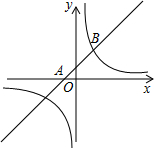 如图,一次函数y=mx+1的图象经过点A(-1,0),且与反比例函数y=$\frac{k}{x}$(k≠0)交于点B(n,2).
如图,一次函数y=mx+1的图象经过点A(-1,0),且与反比例函数y=$\frac{k}{x}$(k≠0)交于点B(n,2).(1)求一次函数和反比例函数的解析式;
(2)求当1≤x≤6时,反比例函数y的取值范围.
分析 (1)把A(-1,0)代入一次函数y=mx+1的解析式即可求得m,即得一次函数的解析式为,把点B(n,2)代入一次函数的解析式,求得B点坐标,把点B的坐标代入y=$\frac{k}{x}$,求得k,得到反比例函数解析式为;
(2)当x=1,x=6时,求出y的值,根据图象求得结论.
解答 解:(1)∵一次函数y=mx+1的图象过点A(-1,0),
∴m=1,
∴一次函数的解析式为:y=x+1
把点B(n,2)带人y=x+1,
∴n=1,
把点B的坐标(1,2)代入y=$\frac{k}{x}$得:k=2
∴反比例函数解析式为:y=$\frac{2}{x}$;
(2)当x=1时,y=$\frac{2}{x}$=2,当x=6时,y=$\frac{2}{x}$=$\frac{1}{3}$,
所以当1≤x≤6时,反比例函数y的取值范围为$\frac{1}{3}$≤y≤2.
点评 此题主要考查了一次函数与反比例函数的交点问题,解题的关键是利用待定系数法求出解析式,再再利用性质求反比例函数y的取值范围.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
17.学校为奖励“汉字听写大赛”的优秀学生,派王老师到商店购买某种奖品,他看到如图所示的关于该奖品的销售信息,便用1400元买回了奖品,求王老师购买该奖品的件数.
| 购买件数 | 销售价格 |
| 不超过30件 | 单价40元 |
| 超过30件 | 每多买1件,购买的所有衬衫单价降低0.5元,但单价不得低于30元 |
16.分式$\frac{2}{x-1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x=1 | C. | x≠-1 | D. | x≠0 |
17.下列图标中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 在反比例函数图象上且到x轴、y轴距离相等.
在反比例函数图象上且到x轴、y轴距离相等.