��Ŀ����
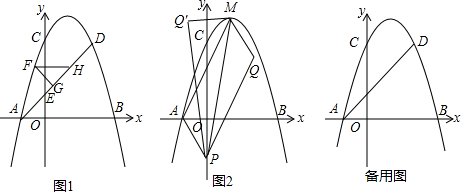
20����ͼ��������y=-x2+2x+3��x�ύ��A��B���㣬��y�ύ�ڵ�C����D��C���������ߵĶԳ���Գƣ�ֱ��AD��y���ཻ�ڵ�E����1����ֱ��AD�Ľ���ʽ��
��2����ͼ1��ֱ��AD�Ϸ�������������һ��F������F��FG��AD�ڵ�G����FHƽ����x�ύֱ��AD�ڵ�H�����FGH�ܳ������ֵ��
��3����ͼ2����M�������ߵĶ��㣬��P��y����һ���㣬��Q������ƽ����һ�㣬�ı���APQM����PMΪ�Խ��ߵ�ƽ���ı��Σ���Q�����Q����ֱ��AM�Գƣ�����M Q�䣬P Q�䣮����PM Q�����APQM�غϲ��ֵ������?APQM�����$\frac{1}{4}$ʱ����?APQM�����
���� ��1�����������߽���ʽ��õ�A��B��C�����꣬�ɵ�D��C���������ߵĶԳ���ԳƵõ�D���꣬�̶����ô���ϵ�������ɵã�
��2�����F��x��-x2+2x+3��������FH��x�ἰֱ��AD�Ľ���ʽy=x+1�ɵõ�H��-x2+2x+2��-x2+2x+3�����̶���ʾ��FH�ij��ȣ����ݶ��κ��������ʿɵ�FH����ֵ������á�FGHΪ����ֱ�������Σ��Ӷ��ɵ����ܳ������ֵ��
��3����P��0��p��������ƽ���ı������ʼ���M����ɵ�Q��2��4+p������P����AM�·���P����AM�Ϸ���������������غϲ��ֵ������ϵ���Գ�����õ�P������ɵ�?APQM�����
��� �⣺��1����-x2+2x+3=0��
���x1=-1��x2=3��
��A��-1��0����C��0��3����
�ߵ�D��C���������ߵĶԳ���Գƣ�
��D��2��3����
��ֱ��AD�Ľ���ʽΪ��y=x+1��
��2�����F��x��-x2+2x+3����
��FH��x�ᣬ
��H��-x2+2x+2��-x2+2x+3����
��FH=-x2+2x+2-x=-��x-$\frac{1}{2}$��2+$\frac{9}{4}$��
��FH�����ֵΪ$\frac{9}{4}$��
��ֱ��AD�Ľ���ʽΪ��y=x+1��֪��DAB=45�㣬
��FH��AB��
���FHG=��DAB=45�㣬
��FG=GH=$\frac{\sqrt{2}}{2}$��$\frac{9}{4}$=$\frac{9\sqrt{2}}{8}$
�ʡ�FGH�ܳ������ֵΪ$\frac{9\sqrt{2}}{8}$��2+$\frac{9}{4}$=$\frac{9+9\sqrt{2}}{4}$��
��3���ٵ�P����AM�·�ʱ����ͼ1��
��P��0��p������֪M��1��4�����Ӷ�Q��2��4+p����
�ߡ�PM Q����?APQM�غϲ��ֵ������?APQM�����$\frac{1}{4}$��
��PQ��ع�AM�е�N��0��2����
���֪Q����y���ϣ�
��֪QQ����е�T�ĺ�����Ϊ1������T����ֱ��AM�ϣ�
��T��1��4�����Ӷ�T��M�غϣ�
��?APQM�Ǿ��Σ�
����ֱ��AM����ʽΪ��y=2x+2��
��MQ��AM��
��ֱ��QQ�䣺y=-$\frac{1}{2}$x+$\frac{9}{2}$��
��4+p=-$\frac{1}{2}$��2+$\frac{9}{2}$��
��ã�p=-$\frac{1}{2}$��
��PN=$\frac{5}{2}$��
��S��APQM=2S��AMP=4S��ANP=4��$\frac{1}{2}$��PN��AO=4��$\frac{1}{2}$��$\frac{5}{2}$��1=5��
�ڵ�P����AM�Ϸ�ʱ����ͼ2��
��P��0��p������֪M��1��4�����Ӷ�Q��2��4+p����
�ߡ�PM Q����?APQM�غϲ��ֵ������?APQM�����$\frac{1}{4}$��
��PQ��ع�QM�е�R��$\frac{3}{2}$��4+$\frac{p}{2}$����
��ֱ��QQ�䣺y=-$\frac{1}{2}$x+p+5��
����$\left\{\begin{array}{l}y=2x+2\\ y=-\frac{1}{2}x+p+5\end{array}$��
��ã�x=$\frac{6+2p}{5}$��y=$\frac{22+4p}{5}$��
��H��$\frac{6+2p}{5}$��$\frac{22+4p}{5}$����
��HΪQQ���е㣬
����Q�䣨$\frac{2+4p}{5}$��$\frac{24+3p}{5}$����
��P��0��p����R��$\frac{3}{2}$��4+$\frac{p}{2}$����ֱ��PR����ʽΪ��y=��$\frac{8}{3}$-$\frac{p}{3}$��x+p��
��Q�䣨$\frac{2+4p}{5}$��$\frac{24+3p}{5}$�����뵽y=��$\frac{8}{3}$-$\frac{p}{3}$��x+p�ã�$\frac{24+3p}{5}$=��$\frac{8}{3}$-$\frac{p}{3}$����$\frac{2+4p}{5}$+p��
�����ã�p2-9p+14=0��
���p1=7��p2=2����AM�е�N�غϣ���ȥ����
��P��0��7����
��PN=5��
��S��APQM=2S��AMP=2��$\frac{1}{2}$��PN��|xM-xA|=2��$\frac{1}{2}$��5��2=10��
����������?APQM���Ϊ5��10��
���� ������Ҫ�������ϵ������������ʽ�����κ��������ʡ�ƽ���ı��ε���������ε��ж������ʵ�֪ʶ�㣬���ݵ�P��λ�÷������ۼ�������֪���������P�������ǽ��������ѵ㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 4cm | B�� | 2cm | C�� | 4cm��2cm | D�� | 8cm |
| A�� | 90�� | B�� | 100�� | C�� | 110�� | D�� | 105�� |