题目内容
5．先化简分式：（$\frac{{x}^{2}-2x+4}{x-1}$+2-x）÷$\frac{{x}^{2}-4}{1-x}$，然后在-2，-1，0，1，2中选一个合适的代入求值．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x=0代入计算即可求出值．
解答 解：原式=$\frac{{x}^{2}-2x+4+（2-x）（x-1）}{x-1}$•$\frac{1-x}{（x+2）（x-2）}$=$\frac{x+2}{x-1}$•$\frac{-（x-1）}{（x+2）（x-2）}$=-$\frac{1}{x-2}$，
当x=0时，原式=$\frac{1}{2}$．
点评 此题考查了分式的化简运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天练口算系列答案
相关题目
16．分式$\frac{2}{x-1}$有意义，则x的取值范围是（ ）
| A． | x≠1 | B． | x=1 | C． | x≠-1 | D． | x≠0 |
如图，秋千链子的长度OA=3m，静止时秋千踏板处于A位置．此时踏板距离地面0.3m，秋千向两边摆动．当踏板处于A′位置时，摆角最大，即∠AOA′=50°，则在A′位置，踏板与地面的距离为1.37m．（sin50°≈0.766，cos50°≈0.6428，结果精确到0.01m）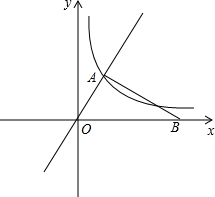
如图，在平面直角坐标系xOy中，已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于点A，且点A的横坐标为1，点B是x轴正半轴上一点，且AB⊥OA．
17．下列图标中，既是中心对称图形又是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
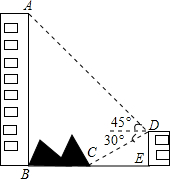如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）