题目内容
12.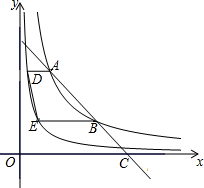 如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为$\frac{9}{2}$.
如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为$\frac{9}{2}$.
分析 根据点A、B在反比例函数y=$\frac{8}{x}$(x>0)的图象上,可设出点B坐标为($\frac{8}{m}$,m),再根据B为线段AC的中点可用m表示出来A点的坐标,由AD∥x轴、BE∥x轴,即可用m表示出来点D、E的坐标,结合梯形的面积公式即可得出结论.
解答 解:∵点A、B在反比例函数y=$\frac{8}{x}$(x>0)的图象上,
设点B的坐标为($\frac{8}{m}$,m),
∵点B为线段AC的中点,且点C在x轴上,
∴点A的坐标为($\frac{4}{m}$,2m).
∵AD∥x轴、BE∥x轴,且点D、E在反比例函数y=$\frac{2}{x}$(x>0)的图象上,
∴点D的坐标为($\frac{1}{m}$,2m),点E的坐标为($\frac{2}{m}$,m).
∴S梯形ABED=$\frac{1}{2}$($\frac{4}{m}-\frac{1}{m}$+$\frac{8}{m}-\frac{2}{m}$)×(2m-m)=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及梯形的面积,解题的关键是用m表示出来A、B、E、D四点的坐标.本题属于基础题,难度不大,解决该题型题目时,只要设出一个点的坐标,再由该点坐标所含的字母表示出其他点的坐标即可.

练习册系列答案
相关题目
2. 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
7.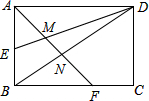 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )| A. | $\frac{2\sqrt{2}}{5}$ | B. | $\frac{9\sqrt{2}}{20}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{4\sqrt{2}}{5}$ |
10.下列各组线段中,不能构成三角形的是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
 如图,⊙O的直径AB⊥弦CD,垂足为点E,连接AC,若CD=2$\sqrt{3}$,∠A=30°,则⊙O的半径为2.
如图,⊙O的直径AB⊥弦CD,垂足为点E,连接AC,若CD=2$\sqrt{3}$,∠A=30°,则⊙O的半径为2.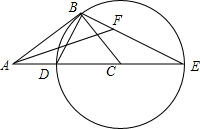 如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.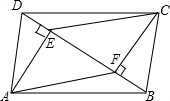 四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.
四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.