题目内容
11.若A=(2-1)(2+1)(22+1)(24+1)…(232+1)+1,则A的个位数字是6.分析 A利用平方差公式化简,归纳总结得到结果个位数字即可.
解答 解:A=(2-1)(2+1)(22+1)(24+1)…(232+1)+1
=(22-1)(22+1)(24+1)…(232+1)+1
=(24-1)(24+1)…(232+1)+1
=264-1+1
=264,
∵21=2,22=4,23=8,24=16,
∴结果个位数以2,4,8,6循环,
则A的个位数字是6,
故答案为:6
点评 此题考查了平方差公式,去括号与添括号,以及完全平方公式,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目
2.下列语句:
①相等的角是对顶角;
②同位角相等;
③若∠1与∠2的两边分别平行,则∠1=∠2;
④两个互补的角中必有一个是钝角;
⑤一个锐角的余角一定小于这个角的补角.
其中正确的个数是( )
①相等的角是对顶角;
②同位角相等;
③若∠1与∠2的两边分别平行,则∠1=∠2;
④两个互补的角中必有一个是钝角;
⑤一个锐角的余角一定小于这个角的补角.
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.若am=3,an=2,则am-2n的值为( )
| A. | 12 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
20.下列图形中,经过折叠不能围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
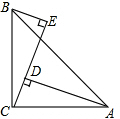 已知:∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,证明:AD=DE+BE.
已知:∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,证明:AD=DE+BE.