Question

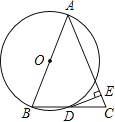
【题目】如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，过点D作⊙O的切线交AC于点E．

（1）求证：DE⊥AC；

（2）若AB=3DE，求tan∠ACB的值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题（1）连接OD，可以证得DE⊥OD，然后证明OD∥AC即可证明DE⊥AC；

（2）利用△ADE∽△CDE，求出DE与CE的比值即可．

试题解析: （1）证明：连接OD，

∵D是BC的中点，OA=OB，

∴OD是△ABC的中位线，

∴OD∥AC，

∵DE是⊙O的切线，

∴OD⊥DE，

∴DE⊥AC；

（2）解：连接AD，

∵AB是⊙O的直径，

∴∠ADB=90°，

∵DE⊥AC，

∴∠ADC=∠DEC=∠AED=90°，

∴∠ADE=∠DCE

在△ADE和△CDE中，

∴△CDE∽△ADE，

∴，

设tan∠ACB=x，CE=a，则DE=ax，AC=3ax，AE=3ax﹣a，

∴，整理得：x2﹣3x+1=0，

解得：x=，

∴tan∠ACB=．