Question

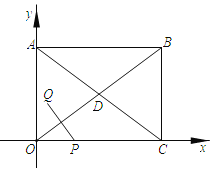
【题目】如图，在平面直角坐标系xOy中，矩形OABC的顶点B坐标为（8，6），对角线AC，BO交于点D，在边OC上有一动点P，点Q是点P关于OB的对称点，设OP＝t．

（1）当PQ过点D时，求点Q的坐标．

（2）用含t的代数式表示点Q的坐标．

（3）过点P作AC的垂线，交△ABC的边于点R，当△PQR为直角三角形时，求t的值．

Answer 1

【答案】（1）点Q的坐标为（，6）；（2）；（3）t的值是或 或 ．

【解析】

根据题目描述，当PQ过点D时，点Q在AB上可以直接解答第一问;通过过Q作QH⊥x轴于H，交OB于E，设PQ交OB于F，进而证明△OFP∽△OCB可用含t的表达式来表示点Q坐标；根据第二问表达式直接分类讨论第三问.

解：（1）如图1，PQ过点D，连接OQ，

∵点Q是点P关于OB的对称点，

∴DQ＝PD，OB⊥PQ，即Q在AB上，

∴OQ＝OP＝t，

∵四边形OABC是矩形，

∴OD＝BD，

∵PQ⊥OB，

∴OQ＝BQ＝t，

∴AQ＝8﹣t，

在Rt△AOQ中，OQ2＝AQ2+OA2，

∴t2＝62+（8﹣t）2，

t＝，

∴AQ＝8﹣＝，

∴点Q的坐标为（，6）；

（2）如图2，过Q作QH⊥x轴于H，交OB于E，设PQ交OB于F，

∵∠FOP＝∠BOC，∠OFP＝∠OCB＝90°，

∴△OFP∽△OCB，

∴

∴，PF＝，

∴PQ＝2PF＝，

sin∠HQP＝＝sin∠BOC＝，

∴，PH＝，

cos∠HQP＝，QH＝，

∴Q（，）；

（3）分3种情况：

①当PR⊥AC于R时，过Q作QH⊥OC于H，

由（2）知：Q（，），

∴CH＝8﹣，QH＝，

∴tan∠ACO＝，

∴，t＝；

②当∠PRQ＝90°时，R在边BC上，如图4，延长CB，过Q作QF⊥CB于F，

∵PR⊥AC，PR⊥QR，

∴AC∥QR，

∴∠QRB＝∠ACB，

∴tan∠QRB＝tan∠ACB＝，

t＝；

③当∠PQR＝90°，R在AB上，如图5，PR⊥AC于F，

∵PQ⊥OB，PQ⊥RQ，

∴EF∥RQ，

∴RF＝PF，

∵BR∥OP，

∴∠RBF＝∠FOP，

∵∠RFB＝∠OFP，

∴△RFB≌△PFO（AAS），

∴OF＝BF，

∵OD＝BD，

∴D与F重合，

Rt△PFC中，PC＝8﹣t，

cos∠ACO＝，

∴，t＝，

综上，t的值是或或．