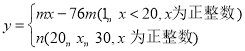题目内容
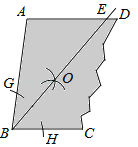
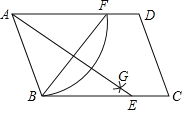
【题目】如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，AB长为半径画弧，交边AD于点；②再分别以B，F为圆心画弧，两弧交于平行四边形ABCD内部的点G处；③连接AG并延长交BC于点E，连接BF，若BF＝3，AB＝2.5，则AE的长为（ ）
A.2B.4C.8D.5
【答案】B
【解析】
连接EF，先证AF=AB=BE，得四边形ABEF是菱形，据此知AE与BF互相垂直平分，继而得OB的长，由勾股定理求得OA的长，继而得出答案．
由题意得：AF=AB，AE为∠BAD的角平分线，则∠BAE=∠FAE．
又∵四边形ABCD是平行四边形，则AD∥BC，∠BAE=∠FAE=∠BEA，∴AF=AB=BE．
连接EF，则四边形ABEF是菱形，∴AE与BF互相垂直平分，设AE与BF相交于点O，OB
1.5．在Rt△AOB中，OA
2，则AE=2OA=4．
故选B．
练习册系列答案
相关题目
【题目】某市A，B两个蔬菜基地得知四川C，D两个灾民安置点分别急需蔬菜240t和260t的消息后，决定调运蔬菜支援灾区，已知A蔬菜基地有蔬菜200t，B蔬菜基地有蔬菜300t，现将这些蔬菜全部调运C，D两个灾区安置点.从A地运往C，D两处的费用分别为每吨20元和25元，从B地运往C，D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
（1）请填写下表，并求两个蔬菜基地调运蔬菜的运费相等时x的值；
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
（2）设A，B两个蔬菜基地的总运费为w元，求出w与x之间的函数关系式，并求
总运费最小的调运方案；
（3）经过抢修，从B地到C处的路况得到进一步改善，缩短了运输时间，运费每吨减少m元（m＞0），其余线路的运费不变，试讨论总运费最小的调动方案.
