题目内容
3.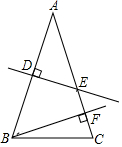 如图,△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,EC的垂直平分线恰好经过点B.求∠A的度数.
如图,△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,EC的垂直平分线恰好经过点B.求∠A的度数.
分析 先根据等腰三角形的性质得出∠ABC=∠C,再由垂直平分线的性质得出∠A=∠ABE,根据CE的垂直平分线正好经过点B,与AC相交于点可知△BCE是等腰三角形,故BF是∠EBC的平分线,故$\frac{1}{2}$(∠ABC-∠A)+∠C=90°,把所得等式联立即可求出∠A的度数.
解答  解:连接BE.
解:连接BE.
∵DE垂直平分AB,EC的垂直平分线恰好经过点B,
∴AE=BE=BC,
∴∠A=∠ABE∠BEC=∠BCE,
∵AB=AC,
∴∠ABC=∠C,
∴∠ABC=∠C=∠BEC,
∵∠BEC=∠A+∠ABE=2∠A,
∴∠ABC=∠C=∠BEC=2∠A,
设:∠A=x°,
则 2x+2x+x=360,
x=36,
∴∠A=36°.
点评 本题考查的是线段垂直平分线的性质及等腰三角形的性质,解答此类问题时往往用到三角形的内角和为180°这一隐含条件.

练习册系列答案
相关题目
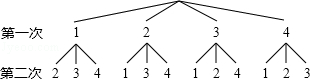
15.在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
小华列出表格如下:
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);
(3)规定两次抽到的数字之和为奇数的获胜,按照各自的规则,你认为谁获胜的可能性大?说明理由?
小明画出树状图如图所示:

小华列出表格如下:
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | ① | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);
(3)规定两次抽到的数字之和为奇数的获胜,按照各自的规则,你认为谁获胜的可能性大?说明理由?
 如图,在正方形网格中每个小正方形边长为1,格点△ABC(顶点是网格线的交点)的顶点A、C坐标分别为(-4,5)、(-1,3).
如图,在正方形网格中每个小正方形边长为1,格点△ABC(顶点是网格线的交点)的顶点A、C坐标分别为(-4,5)、(-1,3).
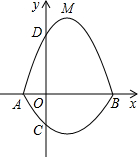 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点.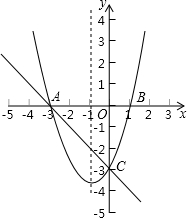 如图:抛物线y1=ax2+bx+c与直线y2=kx+b交于A(-3,0)、C(0,-3)两点,抛物线与x轴交于另一点B(1,0).利用图象填空:
如图:抛物线y1=ax2+bx+c与直线y2=kx+b交于A(-3,0)、C(0,-3)两点,抛物线与x轴交于另一点B(1,0).利用图象填空: