题目内容
13. 如图,在正方形网格中每个小正方形边长为1,格点△ABC(顶点是网格线的交点)的顶点A、C坐标分别为(-4,5)、(-1,3).
如图,在正方形网格中每个小正方形边长为1,格点△ABC(顶点是网格线的交点)的顶点A、C坐标分别为(-4,5)、(-1,3).(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′;
(3)写出△ABC关于x轴对称的△A′′B′′C′′的顶点坐标.
分析 (1)利用点A和点C的坐标画直角坐标系;
(2)利用关于y轴的点的坐标特征,写出A′、B′、C′的坐标,然后描点即可得到△A′B′C′;
(3)利用关于x轴的点的坐标特征,写出A″、B″、C″的坐标.
解答 解:(1)如图,
(2)如图,△A′B′C′为所作;
(3)A′′(-4,-5),B′′(-2,-1),C′′(-1,-3).
点评 本题考查了作图-轴对称变换:画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,一般的方法是:由已知点出发向所给直线作垂线,并确定垂足;直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;连接这些对称点,就得到原图形的轴对称图形.记住关于坐标轴对称的点的坐标特征.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
2.下列式子中,错误的事( )
| A. | $\frac{1-{a}^{2}}{-a}$=$\frac{{a}^{2}-1}{a}$ | B. | $\frac{-1-{a}^{2}}{-a}$=$\frac{1-{a}^{2}}{a}$ | ||
| C. | $\frac{-ab}{a-b}$=$\frac{ab}{b-a}$ | D. | $\frac{(a-b)^{2}}{{a}^{2}-{b}^{2}}$=$\frac{a-b}{a+b}$ |
 如图,△ABC中,∠B=22.5°,AB的垂直平分线交BC于D,AE⊥BC于E,DF⊥AC于F,与AE交于点G.
如图,△ABC中,∠B=22.5°,AB的垂直平分线交BC于D,AE⊥BC于E,DF⊥AC于F,与AE交于点G.
 如图所示,在△ABC中,DE∥BC,AD=6,AB=9,AE=4,则AC的长为多少?
如图所示,在△ABC中,DE∥BC,AD=6,AB=9,AE=4,则AC的长为多少? 如图,C、D是线段AB上的点,E为AD中点,F为BC中点.
如图,C、D是线段AB上的点,E为AD中点,F为BC中点.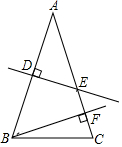 如图,△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,EC的垂直平分线恰好经过点B.求∠A的度数.
如图,△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,EC的垂直平分线恰好经过点B.求∠A的度数.