题目内容
11.已知二次函数y=x2-2x-3与x轴交于A、B两点(A点在B点的左边).(1)求A、B两点的坐标;
(2)在抛物线上存在一点P使△ABP的面积为10,请求出点P的坐标.
分析 (1)令y=0求得x即可得;
(2)根据△ABP的面积为10求得P点纵坐标的绝对值,再由y=5或y=-5分别求出x即可得.
解答 解:(1)令y=0得:x2-2x-3=0,
解得:x=-1或x=3,
∴点A(-1,0)、B(3,0);
(2)∵AB=4,且S△ABP=10,
∴$\frac{1}{2}$AB•|yP|=10,即$\frac{1}{2}$×4•|yP|=10,
解得:|yP|=5,
当y=5时,由x2-2x-3=5,得:x=-2或x=4,
即点P坐标为(-2,5)或(4,5),
当y=-5时,x2-2x-3=-5,方程无解;
综上,P点坐标为(-2,5)或(4,5).
点评 本题主要考查抛物线与x轴的交点,根据三角形的面积求得点P的纵坐标是解题的关键.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
2.下列式子中,错误的事( )
| A. | $\frac{1-{a}^{2}}{-a}$=$\frac{{a}^{2}-1}{a}$ | B. | $\frac{-1-{a}^{2}}{-a}$=$\frac{1-{a}^{2}}{a}$ | ||
| C. | $\frac{-ab}{a-b}$=$\frac{ab}{b-a}$ | D. | $\frac{(a-b)^{2}}{{a}^{2}-{b}^{2}}$=$\frac{a-b}{a+b}$ |

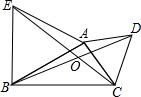 如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.
如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.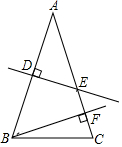 如图,△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,EC的垂直平分线恰好经过点B.求∠A的度数.
如图,△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,EC的垂直平分线恰好经过点B.求∠A的度数.