题目内容
17.已知二次函数y=-ax2+2ax+m的图象与x轴的一个交点是(3,0),则关于x的一元二次方程-ax2+2ax+m=0的解为-1或3..分析 求出抛物线对称轴,利用抛物线与x轴交点关于对称轴对称解决问题.
解答 解:∵二次函数y=-ax2+2ax+m的对称轴x=-$\frac{2a}{-2a}$=1,
又∵抛物线与x轴的两个交点(3,0),
∴另一个交点(-1,0),
∴的一元二次方程-ax2+2ax+m=0的解为x=-1或3,
故答案为-1或3.
点评 本题考查抛物线与x轴的交点,理解二次函数与一元二次方程的关系是解决问题的关键,抛物线与x轴的交点的横坐标就是一元二次方程的解,属于中考常考题型.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
6.计算x3•x3的结果是( )
| A. | 2x3 | B. | 2x6 | C. | x6 | D. | x9 |
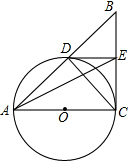 以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于D,E是另一条直角边BC的中点.
以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于D,E是另一条直角边BC的中点.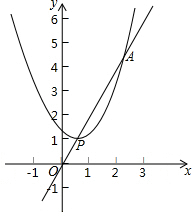 如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.
如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.