题目内容
15.已知抛物线C1:y=-x2+4x-3,把抛物线C1先向右平移3个单位长度,再向上平移3个单位长度,得到抛物线C2,将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M.若直线y=kx+$\frac{1}{2}$与图象M至少有2个不同
的交点,则k的取值范围是0≤k<$\frac{7}{10}$.
分析 首先配方得出二次函数顶点式,求得抛物线C1的顶点坐标,进而利用二次函数平移规律得出抛物线C2,求得顶点坐标,把两点顶点坐标代入即可求得.
解答 解:y=-x2+4x-3=-(x-2)2+1,
∴顶点(2,1)
则将抛物线y=-x2+4x-3先向右平移3个单位长度,再向上平移3个单位长度,
得到的新的抛物线的解析式为:y=(x-5)2+4.
∴顶点(5,4),
把(2,1)代入y=kx+$\frac{1}{2}$(k≥0)得,1=2k+$\frac{1}{2}$,
解得k=$\frac{1}{4}$,
把(5,4)代入y=kx+$\frac{1}{2}$(k≥0)得,4=5k+$\frac{1}{2}$,
解得k=$\frac{7}{10}$,
∴直线y=kx+$\frac{1}{2}$(k≥0)与图象M至少有2个不同的交点,则k的取值范围是0≤k<$\frac{7}{10}$.
故答案为:0≤k<$\frac{7}{10}$.
点评 此题主要考查了二次函数的图象与几何变换,正确利用配方法求出二次函数顶点式的形式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
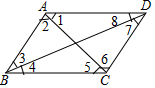 如图,若AD∥BC,则∠1=∠5,∠8=∠4,∠ABC+∠BAC=180°;若DC∥AB,则∠3=∠7,∠2=∠6,∠ABC+∠BCD=180.
如图,若AD∥BC,则∠1=∠5,∠8=∠4,∠ABC+∠BAC=180°;若DC∥AB,则∠3=∠7,∠2=∠6,∠ABC+∠BCD=180.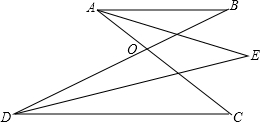 如图,AB∥CD,AC、BD交于点O,∠A、∠D的角平分线交于点E,已知∠E=50°,求∠AOB的度数.
如图,AB∥CD,AC、BD交于点O,∠A、∠D的角平分线交于点E,已知∠E=50°,求∠AOB的度数.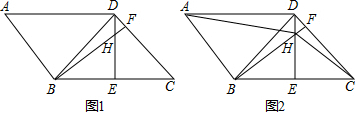
 图象过点A(0,3)B(2,4).题目中的矩形部分是一段因墨水污染而无法辨认的文字.
图象过点A(0,3)B(2,4).题目中的矩形部分是一段因墨水污染而无法辨认的文字.