题目内容
1.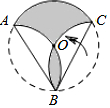 如图,将半径为6的圆形纸片,分别沿AB、BC折叠,若弧AB和弧BC折后都经过圆心O,则阴影部分的面积是12π(结果保留π)
如图,将半径为6的圆形纸片,分别沿AB、BC折叠,若弧AB和弧BC折后都经过圆心O,则阴影部分的面积是12π(结果保留π)
分析 作OD⊥AB于点D,连接AO,BO,CO,求出∠OAD=30°,得到∠AOB=2∠AOD=120°,进而求得∠AOC=120°,再利用阴影部分的面积=S扇形AOC得出阴影部分的面积是⊙O面积的$\frac{1}{3}$,即可得出结果.
解答 解:作OD⊥AB于点D,连接AO,BO,CO,如图所示: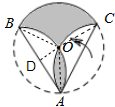
∵OD=$\frac{1}{2}$AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=$\frac{1}{3}$×⊙O面积=$\frac{1}{3}$×π×62=12π;
故答案为:12π.
点评 本题主要考查了翻折变换的性质、扇形面积以及圆的面积公式等知识;解题的关键是确定∠AOC=120°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.观察下列立体图形,左视图为矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.下列运算结果正确的是( )
| A. | a2+a3=a5 | B. | a3÷a2=a | C. | a2•a3=a6 | D. | (a2)3=a5 |
16.下列四个实数中,无理数是( )
| A. | 3.14 | B. | -π | C. | 0 | D. | $\sqrt{9}$ |
6. 由6个完全相同的小正方体组成的立体图形如图所示,则在以下视图中,与其它三个形状都不同的是( )
由6个完全相同的小正方体组成的立体图形如图所示,则在以下视图中,与其它三个形状都不同的是( )
 由6个完全相同的小正方体组成的立体图形如图所示,则在以下视图中,与其它三个形状都不同的是( )
由6个完全相同的小正方体组成的立体图形如图所示,则在以下视图中,与其它三个形状都不同的是( )| A. | 主视图 | B. | 俯视图 | C. | 左视图 | D. | 右视图 |
13.下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线相等且垂直的四边形是正方形 | |
| C. | 平行四边形的对角线互相平分 | |
| D. | 对角线相等的四边形是矩形 |
 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )