题目内容
4.(1)计算$\sqrt{8}$+|($\sqrt{3}-1$)0-2sin45°|+2-1(2)解方程:$\frac{x}{x-1}$-2=$\frac{2}{{x}^{2}+x-2}$.
分析 (1)原式利用二次根式性质,绝对值的代数意义,零指数幂、负整数指数幂法则计算即可得到结果;
(2)分式去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{2}$-1+$\frac{1}{2}$=3$\sqrt{2}$-$\frac{1}{2}$;
(2)去分母得:x2+2x-2x2-2x+4=2,即x2=2,
解得:x=±$\sqrt{2}$,
经检验x=±$\sqrt{2}$都为分式方程的解.
点评 此题考查了实数的运算,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.-3的倒数的绝对值是( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 正方形 | D. | 圆 |
19.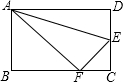 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | 5 |
9.|-6|的相反数是( )
| A. | -6 | B. | 6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |