题目内容
7.一个不透明的袋中装有2只红球和2只绿球,这些球除颜色外完全相同.(1)从袋中一次随机摸出1只球,则这只球是红球的概率为$\frac{1}{2}$;
(2)从袋中一次随机摸出2只球,求这2只球颜色不同的概率.
分析 (1)直接利用概率公式计算;
(2)画树状图展示所有12种等可能的结果数,再找出这2只球颜色不同的结果数,然后根据概率公式计算.
解答 解:(1)从袋中一次随机摸出1只球,则这只球是红球的概率=$\frac{2}{4}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$;
(2)画树状图为:
共有12种等可能的结果数,其中这2只球颜色不同的结果数为8,
所以这2只球颜色不同的概率=$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
17.在平面直角坐标系中,将点A(m-1,n+2)先向右平移3个单位,再向上平移2个单位,得到点A′,若点A′位于第二象限,则m、n的取值范围分别是( )
| A. | m<0,n>0 | B. | m<1,n>-2 | C. | m<0,n<-2 | D. | m<-2,m>-4 |
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 正方形 | D. | 圆 |
19.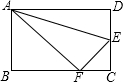 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | 5 |
17. 如图,△ABC内接于⊙O,若⊙O的半径为2,∠A=45°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为2,∠A=45°,则$\widehat{BC}$的长为( )
 如图,△ABC内接于⊙O,若⊙O的半径为2,∠A=45°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为2,∠A=45°,则$\widehat{BC}$的长为( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)