题目内容
19．双休日，小明在家做功课、做家务和户外活动时间之比是4：1：3．如果设他做家务的时间是x小时，又知道这三方面总共花了8小时，那么可列出的方程是x+4x+3x=8．分析 设小明做家务的时间是x小时，则根据做功课、做家务和户外活动时间之比是4：1：3，可求出做功课时间为：4x，户外活动时间为：3x，然后再根据这三方面总共花了8小时列出方程求解即可．
解答 解：设小明做家务的时间是x小时，
∵小明在家做功课、做家务和户外活动时间之比是4：1：3，
∴小明做功课时间为：4x，户外活动时间为：3x，
∴x+4x+3x=8，
故答案为：x+4x+3x=8．
点评 本题考查了由实际问题抽象出一元一次方程，解答本题的关键在于熟读题意，根据题中所给的条件列出一元一次方程．
练习册系列答案
相关题目
7．
实数x、y在数轴上的对应点的位置如图，把-x、-y、0按照从小到大的顺序排列，正确的是（ ）
实数x、y在数轴上的对应点的位置如图，把-x、-y、0按照从小到大的顺序排列，正确的是（ ）| A． | -x＜0＜y | B． | -y＜0＜-x | C． | 0＜-x＜-y | D． | 0＜-y＜-x |
如图所示，已知点A的坐标为（1，0），C，B两点分别在x轴、y轴上移动，且∠1=45°，则点B坐标为（0，-$\sqrt{2}$）时，BC与⊙O相切．
4．某厂今年3月份的产量是a吨，比同年2月份产量增加20%，则2月份的产量（ ）
| A． | 1.2a吨 | B． | 0.8a吨 | C． | $\frac{5}{6}a$吨 | D． | 0.2a吨 |
11．已知在△AB中，∠C=90°，AB=13，BC=12，那么∠A的正弦值是（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{12}{5}$ | C． | $\frac{5}{13}$ | D． | $\frac{12}{13}$ |
8．
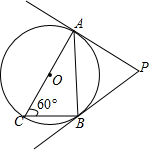如图，AC是⊙0的直径，∠ACB=60°，连接AB，过A，B两点分别作⊙O的切线，两切线交于点P．若已知⊙O半径为1，则△PAB的周长为（ ）
如图，AC是⊙0的直径，∠ACB=60°，连接AB，过A，B两点分别作⊙O的切线，两切线交于点P．若已知⊙O半径为1，则△PAB的周长为（ ）| A． | 3$\sqrt{3}$ | B． | $\frac{3\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | 3 |
9．
如图，在?ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（ ）
如图，在?ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（ ）| A． | $3-\frac{π}{3}$ | B． | $3-\frac{π}{6}$ | C． | $4-\frac{π}{3}$ | D． | $4-\frac{π}{6}$ |