题目内容
1.现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于290元,问有几种购买方案,哪种方案费用最低?
分析 (1)设A商品每件x元,B商品每件y元,根据关系式列出二元一次方程组.
(2)设小亮准备购买A商品a件,则购买B商品(10-a)件,根据关系式列出二元一次不等式方程组.求解再比较两种方案.
解答 解:(1)设A商品每件x元,B商品每件y元,
依题意,得$\left\{\begin{array}{l}{2x+y=90}\\{3x+2y=160}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=20}\\{y=50}\end{array}\right.$.
答:A商品每件20元,B商品每件50元.
(2)设小亮准备购买A商品a件,则购买B商品(10-a)件
$\left\{\begin{array}{l}{20a+50(10-a)≥290}\\{20a+50(10-a)≤350}\end{array}\right.$
解得5≤a≤7,
根据题意,a的值应为整数,所以a=5、a=7或a=6.
方案一:当a=5时,购买费用为20×5+50×(10-5)=350元;
方案二:当a=6时,购买费用为20×6+50×(10-6)=320元;
方案三:当a=6时,购买费用为20×7+50×(10-7)=290元;
∵350>290
∴购买A商品7件,B商品3件的费用最低.
答:有三种购买方案,方案一:购买A商品5件,B商品5件;方案二:购买A商品6件,B商品4件,方案三:购买A商品7件,B商品3件,其中方案三费用最低.
点评 此题主要考查二元一次方程组及二元一次不等式方程组的应用,关键是根据题意得出关系式得出A商品每件20元,B商品每件50元.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
17.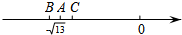 如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
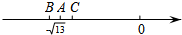 如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )| A. | 4和5 | B. | -5和-4 | C. | 3和4 | D. | -4和-3 |
11.《中华人民共和国个人所得税法》规定,公民月工资所得不超过1600元
(人民币)的部分不必纳税,超过1600元的部分为各月应纳税所得额,超过部分的税款按下表分段累加计算.例如,你月工资是2000元,2000-1600=400,那么就对400元进行纳税,400×5%=20,即你应交纳的税款为20元.若某人1月份应交纳此项税款92元,则她当月的工资是多少?
(人民币)的部分不必纳税,超过1600元的部分为各月应纳税所得额,超过部分的税款按下表分段累加计算.例如,你月工资是2000元,2000-1600=400,那么就对400元进行纳税,400×5%=20,即你应交纳的税款为20元.若某人1月份应交纳此项税款92元,则她当月的工资是多少?
| 全月应纳税所得额 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500元至2000元的部分 | 10% |
| 超过2000元至5000元的部分 | 15% |
| 超过5000元至20000元的部分 | 20% |
| … | … |
 如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.
如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.