题目内容
9.计算题:(1)解方程:4(2-x)-3(x+1)=6
(2)解方程:$\frac{x+3}{6}$=1-$\frac{3-2x}{4}$
(3)解方程组:$\left\{\begin{array}{l}3x+2y=-1\\ x+4y=-7\end{array}\right.$
(4)解方程组:$\left\{\begin{array}{l}4(x+2)=1-5y\\ 3(y+2)=3-2x\end{array}\right.$.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程组利用加减消元法求出解即可;
(4)方程组利用加减消元法求出解即可.
解答 解:(1)去括号得:8-4x-3x-3=6,
移项合并得:-7x=1,
解得:x=-$\frac{1}{7}$;
(2)去分母得:2x+6=12-9+6x,
移项合并得:4x=3,
解得:x=$\frac{3}{4}$;
(3)$\left\{\begin{array}{l}{3x+2y=-1①}\\{x+4y=-7②}\end{array}\right.$,
①×2-②得:5x=5,即x=1,
把x=1代入②得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{4x+5y=-7①}\\{2x+3y=-3②}\end{array}\right.$,
②×2-①得:y=1,
把y=11代入①得:x=-3,
则方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
19.4的平方根是( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
 如图所示,已知函数y=x+b和y=ax-1的图象交点为M,则不等式x+b<ax-1的解集为x<-1.
如图所示,已知函数y=x+b和y=ax-1的图象交点为M,则不等式x+b<ax-1的解集为x<-1.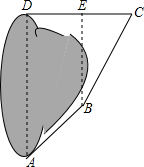 某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192) 如图,汽车在沿坡比为1:5斜坡上前进100$\sqrt{26}$米,则汽车上升的高度BC的长为100m.
如图,汽车在沿坡比为1:5斜坡上前进100$\sqrt{26}$米,则汽车上升的高度BC的长为100m.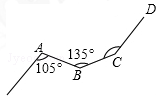 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°. 如图,直线a∥b,∠1=45°,则∠2=45°,∠3=135°.
如图,直线a∥b,∠1=45°,则∠2=45°,∠3=135°.