题目内容
3.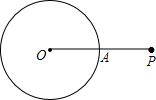 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.甲:以点A为圆心,AP长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:过点A作直线MN⊥OP:以点O为圆心,OP为半径画弧,交射线AM于点B,连接OB,交⊙O于点C,直线CP即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
| A. | 甲正确,乙错误 | B. | 乙正确,甲错误 | C. | 两人都正确 | D. | 两人都错误 |
分析 对于甲的作法,连结OB,如图1,先判断OP为⊙A的直径,再根据圆周角定理得到∠OBP=90°,于是根据切线的判定定理得到PB为⊙O的切线;
对于乙的作法:如图2,通过证明△OAB≌△OCP得到∠OAB=∠OCP=90°,于是根据切线的判定定理得到PC为⊙O的切线.
解答 解:对于甲的作法: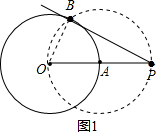
连结OB,如图1,
∵OA=AP,
∴OP为⊙A的直径,
∴∠OBP=90°,
∴OB⊥PB,
∴PB为⊙O的切线,所以甲的说法正确;
对于乙的作法: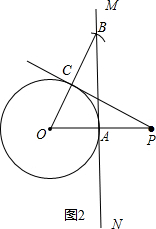
如图2,
∵MN⊥OP,
∴∠OAB=90°,
∵OA=AP,OB=OP,
∴OB=OP,
在△OAB和OCP中
$\left\{\begin{array}{l}{OA=OC}\\{∠AOB=∠COP}\\{OB=OP}\end{array}\right.$,
∴△OAB≌△OCP,
∴∠OAB=∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线,所以乙的说法正确.
故选C.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了作图-复杂作图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.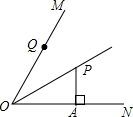 如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
 如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | 2 | D. | $\sqrt{3}$ |
18.已知一元二次方程x2-4=0,则该方程的解为( )
| A. | x1=x2=2 | B. | x1=x2=-2 | C. | x1=-4,x2=4 | D. | x1=-2,x2=2 |

 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2,则△BEF的面积:4cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2,则△BEF的面积:4cm2.
 如图,直线y=2x+3与坐标轴分别交于A、B两点,点P在直线y=x上,且△ABP的面积被y轴平分,求点P的坐标.
如图,直线y=2x+3与坐标轴分别交于A、B两点,点P在直线y=x上,且△ABP的面积被y轴平分,求点P的坐标.