题目内容
15. 如图,直线y=2x+3与坐标轴分别交于A、B两点,点P在直线y=x上,且△ABP的面积被y轴平分,求点P的坐标.
如图,直线y=2x+3与坐标轴分别交于A、B两点,点P在直线y=x上,且△ABP的面积被y轴平分,求点P的坐标.
分析 先根据x轴上点的坐标特征得到A(-$\frac{3}{2}$,0),由于△ABP的面积被y轴平分,则点A和点P到y轴的距离相等,则点P与点A的横坐标互为相反数,即P点的横坐标为$\frac{3}{2}$,从而得到点P的坐标.
解答  解:当y=0时,2x+3=0,解得x=-$\frac{3}{2}$,则A(-$\frac{3}{2}$,0),
解:当y=0时,2x+3=0,解得x=-$\frac{3}{2}$,则A(-$\frac{3}{2}$,0),
∵△ABP的面积被y轴平分,
∴点P与点A的横坐标互为相反数,
∴P点的横坐标为$\frac{3}{2}$,
∴点P的坐标为($\frac{3}{2}$,$\frac{3}{2}$).
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知甲校原有1016人,乙校原有1028人,寒假期间甲、乙两校人数变动的原因只有转出与转入两种,且转出的人数比为1:3,转入的人数比也为1:3.若寒假结束开学时甲、乙两校人数相同,则乙校开学时的人数与原有的人数相差多少?( )
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
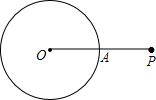 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下. 已知,如图,C是AB的中点,AD∥CE,AD=CE.求证:△ADC≌△CEB.
已知,如图,C是AB的中点,AD∥CE,AD=CE.求证:△ADC≌△CEB.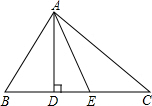 在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°.
在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°. 如图,点O为?ABCD的对角线BD的中点,经过点O的直线分别交BA的延长线,DC的延长线于点E,F,求证:AE=CF.
如图,点O为?ABCD的对角线BD的中点,经过点O的直线分别交BA的延长线,DC的延长线于点E,F,求证:AE=CF.