题目内容
13.如图所示的长方形或正方形三类卡片各有若干张,请你用这些卡片,拼成一个面积是2a2+3ab+b2长方形(要求:所拼图形中每类卡片都要有,卡片之间不能重叠.)画出示意图,并计算出它的面积.

分析 首先根据因式分解的方法,判断出2a2+3ab+b2=(a+b)(2a+b);然后根据长方形的面积公式,判断出面积是2a2+3ab+b2长方形的长是2a+b,宽是a+b即可.
解答 解:2a2+3ab+b2
=(a2+2ab+b2)+(a2+ab)
=(a2+2ab+b2)+a(a+b)
=(a+b)2+a(a+b)
=(a+b)(2a+b)
所以面积是2a2+3ab+b2长方形的长是2a+b,宽是a+b. .
.
点评 (1)此题主要考查了因式分解方法的应用,要熟练掌握,解答此题的关键是要明确:用因式分解的方法将式子变形时,根据已知条件,变形的可以是整个代数式,也可以是其中的一部分.
(2)此题还考查了长方形的面积的求法,要熟练掌握,解答此题的关键是要明确:长方形的面积=长×宽.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
1.已知(-3a+m)(4b+n)=16b2-9a2,则m,n的值分别为( )
| A. | m=-4b,n=3a | B. | m=4b,n=-3a | C. | m=4b,n=3a | D. | m=3a,n=4b |
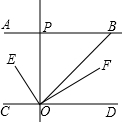 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=$\frac{1}{2}$(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论①②③(填编号).
如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=$\frac{1}{2}$(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论①②③(填编号).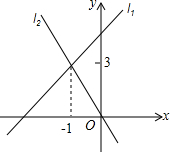 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式0<k2x<k1x+b的解集为-1<x<0.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式0<k2x<k1x+b的解集为-1<x<0.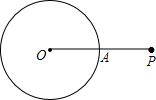 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.