题目内容
适合关系式|x+
|+|x-
|=2的整数解x的个数是( )
| 2 |
| 3 |
| 4 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:含绝对值符号的一元一次方程
专题:
分析:分类讨论:①x>
,②x<-
,③-
<x<
,根据分类讨论,可去掉绝对值,根据解方程,可得答案.
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
解答:解:当x>
时,原式可化为:x+
+x-
=2,解得:x=
,不适合题意舍去;
当x<-
时,原式可化为:-x-
-x+
=2,解得:x=-
,不适合题意舍去;
当-
<x<
时,原式可化为:x+
-x+
=2,解得:2=2.说明当-
<x<
时,关系式|x+
|+|x-
|=2恒成立,
所以满足条件的整数解x有:0和1.
故选:C.
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
当x<-
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
当-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
所以满足条件的整数解x有:0和1.
故选:C.
点评:本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键,注意解要在分类的范围内.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
直线a、b、c是三条平行直线.已知a与b的距离为7cm,b与c的距离为3cm,则a与c的距离为( )
| A、4cm | B、10cm |
| C、3cm | D、4cm或10cm |
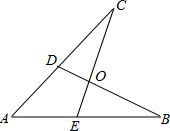 如图,已知AB=AC,要使△ABD≌△ACE,只需补充条件( )
如图,已知AB=AC,要使△ABD≌△ACE,只需补充条件( )| A、∠BOE=∠COD |
| B、∠DOE=∠BOC |
| C、BO=CO |
| D、BO⊥CO |
 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值. 如图,已知∠B=∠C,AD=AE,求证:AB=AC.
如图,已知∠B=∠C,AD=AE,求证:AB=AC.