题目内容
1．两个相似三角形的周长比为1：4，则它们的对应边上的高比为（ ）| A． | 1：2 | B． | 1：4 | C． | 1：8 | D． | 1：16 |
分析 直接根据相似三角形的性质即可得出结论．
解答 解：∵两个相似三角形的周长比为1：4，
∴它们的对应边上的高比为1：4．
故选B．
点评 本题考查的是相似三角形的性质，熟知相似三角形对应高的比等于相似比是解答此题的关键．
练习册系列答案
相关题目
如图，点A在x轴正半轴上，点C在y轴正半轴上，OA=2OC，将矩形OABC绕原点O逆时针旋转90°，得到矩形ODEF．抛物线y=ax2+bx+c经过F、D、B三个点，其顶点在直线y=$\frac{7}{2}$x-$\frac{1}{12}$上，直线L：y=kx+m经过点E和点A，点P是抛物线y=ax2+bx+c上第一象限任意一点，过点P作x轴的垂线交直线L于点M．
9．
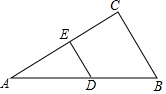如图，在△ABC中，AB=8，∠C=90°，∠A=30°，D、E分别为AB、AC边上的中点，则DE的长为（ ）
如图，在△ABC中，AB=8，∠C=90°，∠A=30°，D、E分别为AB、AC边上的中点，则DE的长为（ ）| A． | 2 | B． | 3 | C． | 2$\sqrt{3}$ | D． | 4 |
16．方程2x（x+6）=5（x+6）的解为（ ）
| A． | x=-6 | B． | x=$\frac{5}{2}$ | C． | x1=-6，x2=$\frac{5}{2}$ | D． | x1=6，x2=-$\frac{5}{2}$ |
10．无理数3$\sqrt{5}$在下面哪两个数之间（ ）
| A． | 3与4 | B． | 4与5 | C． | 5与6 | D． | 6与7 |
11．下列二次根式中，不能与$\sqrt{6}$合并的是（ ）
| A． | $\sqrt{\frac{2}{3}}$ | B． | $\sqrt{24}$ | C． | $\sqrt{1.5}$ | D． | $\sqrt{1.2}$ |