题目内容
10.先化简,再求值:$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=3tan30°+1,b=$\sqrt{2}$cos45°.
分析 直接将原式通分进而分解因式后再化简,把已知代入得出答案.
解答 解:原式=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$=$\frac{1}{a-b}$,
当a=3tan30°+1=3×$\frac{\sqrt{3}}{3}$+1=$\sqrt{3}$+1,
b=$\sqrt{2}$cos45°=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,
原式=$\frac{1}{\sqrt{3}+1-1}$=$\frac{\sqrt{3}}{3}$.
点评 此题主要考查了分式的化简求值,正确进行分式的混合运算是解题关键.

练习册系列答案
相关题目
1.要使多项式x2-2kxy-3y2+$\frac{1}{2}$xy-5x+70不含x、y的乘积项,则k的值为( )
| A. | -$\frac{1}{4}$ | B. | -1 | C. | $\frac{1}{4}$ | D. | 1 |
20.如果a<b<0,那么下列不等式中成立的是( )
| A. | -3a<-3b | B. | a3<b3 | C. | a2<b2 | D. | c-a<c-b |
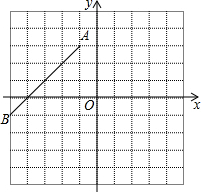 已知,如图平面直角坐标系内,O为坐标原点,A(-1,3),B(-5,-1),连接AB,
已知,如图平面直角坐标系内,O为坐标原点,A(-1,3),B(-5,-1),连接AB, 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF,分别交AD、BC于点E和点F,
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF,分别交AD、BC于点E和点F,