题目内容
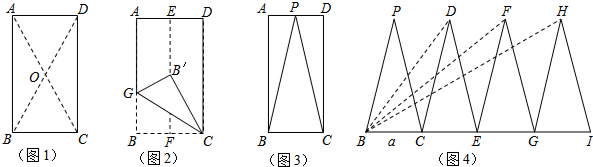
15.数学课上,老师和同学们对矩形纸片进行了图形变换的以下探究活动:(1)如图1,若连接矩形ABCD的对角线AC、BD相交于点O,则Rt△ADC可由Rt△ABC经过旋转变换得到,这种旋转变换的旋转中心是点O、旋转角度是180°;
(2)如图2,将矩形纸片ABCD沿折痕EF对折、展平.再沿折痕GC折叠,使点B落在EF上的点B′处,这样能得到∠B′GC.求∠B′GC的度数.
(3)如图3,取AD边的中点P,剪下△BPC,将△BPC沿着射线BC的方向依次进行平移变换,每次均移动BC的长度,得到了△CDE、△EFG和△GHI(如图4).若BH=BI,BC=a,则:①证明以BD、BF、BH为三边构成的新三角形的是直角三角形;②若这个新三角形面积小于50$\sqrt{15}$,请求出a的最大整数值.
分析 (1)根据矩形是中心对称图形,可以将Rt△ABC旋转180°得到Rt△ADC而得出结论;
(2)连接BB',由题意得EF垂直平分BC,就有BB'=B'C,由翻折可得B'C=BC,从而△BB'C为等边三角形.就可以求出∠B'CB=60°;
(3)分别取CE、EG、GI的中点M、Q、N,连接DM、FQ、HN、BD、BF、BH,由BP=PC,根据平移变换的性质,就有△CDE、△EFG和△GHI都是等腰三角形,就有DM⊥CE,FQ⊥EG,HN⊥GI,由勾股定理就可以求出HN2=$\frac{15}{4}$a2,从而得出新三角形三边的值,从而得出结论.
解答  解:(1)将△ABC绕点O旋转180°后可得到△ADC;
解:(1)将△ABC绕点O旋转180°后可得到△ADC;
故答案为:O、180;
(2)如答图1,连接BB',由题意得EF垂直平分BC,故BB'=B'C,由翻折可得,
B'C=BC,
∴△BB'C为等边三角形.
∴∠B'CB=60°,
(或由三角函数FC:B'C=1:2求出∠B'CB=60°也可以.)
∴∠B'CG=30°,
∴∠B'GC=60°;
(3)①如答图2,分别取CE、EG、GI的中点M、Q、N,连接DM、FQ、HN、BD、BF、BH,
∵△PBC中,PB=PC,根据平移变换的性质,△CDE、△EFG和△GHI都是等腰三角形,
∴DM⊥CE,FQ⊥EG,HN⊥GI.
在Rt△BHN中,BH=BI=4a,
BH2=HN2+BN2,HN2=$\frac{15}{4}$a2,
则DM2=FQ2=HN2=$\frac{15}{4}$a2,
BD2=BM2+DM2=6a2,BF2=BQ2+FQ2=10a2,
新三角形三边长为4a、$\sqrt{6}$a、$\sqrt{10}$a.
∵BH2=BD2+BF2
∴新三角形为直角三角形.
(或通过转换得新三角形三边就是BD、DI、BI,即求△GBI的面积或利用△HBI与△HGI相似,求△HBI的面积也可以).
②其面积为$\frac{1}{2}$$\sqrt{6}$a•$\sqrt{10}$a=$\sqrt{15}$a2.
∵$\sqrt{15}$a2<50$\sqrt{15}$,
∴a2<50
∴a的最大整数值为7.
点评 本题考查了旋转变换的运用,翻折变换的运用,平移变换的运用,等边三角形的性质的运用,勾股定理的运用,等腰三角形的性质的运用,三角形的面积公式的运用.本题的综合性较强要求学生熟练的运用图形变换解题是关键.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案| 行驶时间x(时) | 0 | 1 | 2 | 3 | 4 |
| 余油量y(升) | 150 | 120 | 90 | 60 | 30 |
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
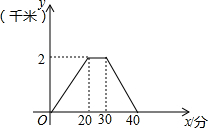 星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )(1)小王去时的速度大于回家的速度;
(2)小王在朋友家停留了10分;
(3)小王去时所花的时间少于回家所花的时间;
(4)小王去时走上坡路,回家时走下坡路.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 0.23×106 | B. | 2.2×104 | C. | 22.8×104 | D. | 2.3×105 |
 如图,如果点M的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )
如图,如果点M的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大为原来的4倍 |

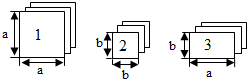 如图,有足够多的长方形和正方形卡片,
如图,有足够多的长方形和正方形卡片,