题目内容
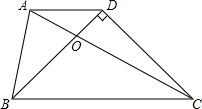 如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.
如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.考点:等腰三角形的判定与性质,等腰直角三角形
专题:证明题
分析:过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,因此AM∥DN,因为AD∥BC,所以DN=AM,根据等腰直角三角形性质得出BC=2DN=2AM,即AC=2AM,由于∠AMC为直角,所以∠ACB=30°,求出∠AOB=75°,∠OAB=75°,根据等角对等边即可得出答案.
解答: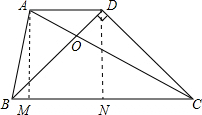 证明:过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,则AM∥DN,
证明:过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,则AM∥DN,
∵AD∥BC,
∴四边形AMND是矩形,
∴DN=AM,
∵BD⊥CD,BD=CD,
∴△BDC为等腰直角三角形,
∴BC=2DN=2AM,
∵AC=BC,
∴AC=2AM,
∵∠AMC为直角,
∴∠ACB=30°,
∴∠AOB=45°+30°=75°,
∵AC=BC,
∴∠CAB=
(180°-∠ACB)=
(180-30)=75°,
∴∠AOB=∠OAB,
∴AB=BO.
 证明:过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,则AM∥DN,
证明:过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,则AM∥DN,∵AD∥BC,
∴四边形AMND是矩形,
∴DN=AM,
∵BD⊥CD,BD=CD,
∴△BDC为等腰直角三角形,
∴BC=2DN=2AM,
∵AC=BC,
∴AC=2AM,
∵∠AMC为直角,
∴∠ACB=30°,
∴∠AOB=45°+30°=75°,
∵AC=BC,
∴∠CAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOB=∠OAB,
∴AB=BO.
点评:本题考查了等腰直角三角形性质,含30度角的直角三角形性质,平行四边形的性质和判定,三角形的内角和定理的应用,综合性比较强,有一定的难度.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

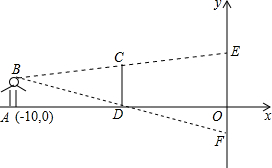 如图,在平面直角坐标系内,小聪站在距离y轴10m点A(-10,0)处观察y轴.眼睛距x轴1.5m,他的前方5m处有一障碍物CD,若CD=2m.求y轴上小聪看不到的EF的长,并求出E、F两点的坐标.
如图,在平面直角坐标系内,小聪站在距离y轴10m点A(-10,0)处观察y轴.眼睛距x轴1.5m,他的前方5m处有一障碍物CD,若CD=2m.求y轴上小聪看不到的EF的长,并求出E、F两点的坐标.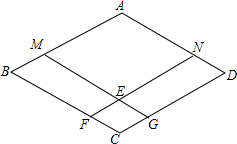 如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN、EFCG都是菱形.
如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN、EFCG都是菱形.