题目内容
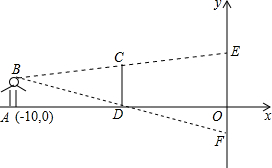 如图,在平面直角坐标系内,小聪站在距离y轴10m点A(-10,0)处观察y轴.眼睛距x轴1.5m,他的前方5m处有一障碍物CD,若CD=2m.求y轴上小聪看不到的EF的长,并求出E、F两点的坐标.
如图,在平面直角坐标系内,小聪站在距离y轴10m点A(-10,0)处观察y轴.眼睛距x轴1.5m,他的前方5m处有一障碍物CD,若CD=2m.求y轴上小聪看不到的EF的长,并求出E、F两点的坐标.考点:相似三角形的应用,坐标与图形性质
专题:
分析:作BH⊥y轴于H,交CD于Q,如图,易得AB=DQ=OH=1.5,CQ=CD-DQ=0.5,BH=10,BQ=5,先证明△BCQ∽△BEH,利用相似比计算出EH=1,则OE=EH+OH=2.5,于是得到E点坐标为(0,2.5);再证明△BDQ∽△BFH,利用相似不计算出HF=3,则OF=HF-OH=1.5,所以F点坐标为(0,-1.5).
解答:解:作BH⊥y轴于H,交CD于Q,如图, AB=DQ=OH=1.5,CQ=CD-DQ=0.5,BH=10,BQ=5,
AB=DQ=OH=1.5,CQ=CD-DQ=0.5,BH=10,BQ=5,
∵CQ∥EH,
∴△BCQ∽△BEH,
∴
=
,即
=
,解得EH=1,
∴OE=EH+OH=2.5,
∴E点坐标为(0,2.5);
∵DQ∥FH,
∴△BDQ∽△BFH,
∴
=
,即
=
,解得HF=3,
∴OF=HF-OH=3-1.5=1.5,
∴F点坐标为(0,-1.5).
 AB=DQ=OH=1.5,CQ=CD-DQ=0.5,BH=10,BQ=5,
AB=DQ=OH=1.5,CQ=CD-DQ=0.5,BH=10,BQ=5,∵CQ∥EH,
∴△BCQ∽△BEH,
∴
| BQ |
| BH |
| CQ |
| EH |
| 5 |
| 10 |
| 0.5 |
| EH |
∴OE=EH+OH=2.5,
∴E点坐标为(0,2.5);
∵DQ∥FH,
∴△BDQ∽△BFH,
∴
| DQ |
| HF |
| BQ |
| BH |
| 1.5 |
| HF |
| 5 |
| 10 |
∴OF=HF-OH=3-1.5=1.5,
∴F点坐标为(0,-1.5).
点评:本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.也考查了坐标与图形性质.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
若一元二次方程ax2+bx+c=0无解,且a<0,则二次函数y=ax2+bx+c的值( )
| A、总大于0 | ||
| B、总小于0 | ||
C、在x>-
| ||
D、在x>-
|
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为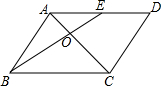 如图,在平行四边形ABCD中,点E为边AD的中点,连接AC、BE交于点O,若AO=3,则AC=
如图,在平行四边形ABCD中,点E为边AD的中点,连接AC、BE交于点O,若AO=3,则AC= 如图,四边形OABC为菱形,点A、B在以O为圆心的弧上,若OA=2,∠1=∠2.
如图,四边形OABC为菱形,点A、B在以O为圆心的弧上,若OA=2,∠1=∠2.
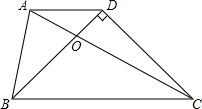 如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.
如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.