题目内容
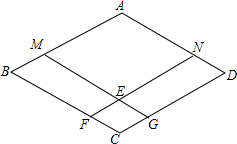 如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN、EFCG都是菱形.
如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN、EFCG都是菱形.考点:菱形的判定与性质
专题:证明题
分析:根据菱形的判定方法证明平行四边形AMEN是菱形和平行四边形EFCG是菱形即可.
解答: 证明:①∵四边形ABCD是菱形,
证明:①∵四边形ABCD是菱形,
∴AB=AD.
又∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∵BM=DN,
∴AB-BC=AD-DN,即AM=AN,
∴四边形AMEN是菱形.
②∵四边形ABCD是菱形,
∴AB=AD=DC=BC,AB∥DC,AD∥BC,
又∵MG∥AD,NF∥AB,
∴MG∥BC,NF∥DC,则EF∥GC,EG∥FC,
∴四边形EFCG是平行四边形.
∴EF=CG,EG=FC,
∵BM=DN,BM=CG,DN=FC,
∴FC=CG,
∴四边形EFCG是菱形.
 证明:①∵四边形ABCD是菱形,
证明:①∵四边形ABCD是菱形,∴AB=AD.
又∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∵BM=DN,
∴AB-BC=AD-DN,即AM=AN,
∴四边形AMEN是菱形.
②∵四边形ABCD是菱形,
∴AB=AD=DC=BC,AB∥DC,AD∥BC,
又∵MG∥AD,NF∥AB,
∴MG∥BC,NF∥DC,则EF∥GC,EG∥FC,
∴四边形EFCG是平行四边形.
∴EF=CG,EG=FC,
∵BM=DN,BM=CG,DN=FC,
∴FC=CG,
∴四边形EFCG是菱形.
点评:本题考查了菱形的判定与性质.解题的关键是熟记各种特殊四边形的判定和性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组单项式中,不是同类项的是( )
A、12y与
| ||||
| B、6mb与-bm | ||||
| C、23与32 | ||||
D、
|
若一元二次方程ax2+bx+c=0无解,且a<0,则二次函数y=ax2+bx+c的值( )
| A、总大于0 | ||
| B、总小于0 | ||
C、在x>-
| ||
D、在x>-
|
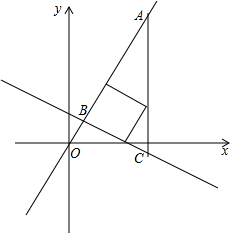 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-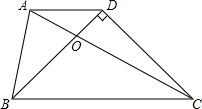 如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.
如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.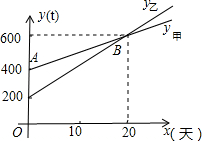 如图,AB、CB表示某工厂甲、乙两车间的产量y(t)与所用时间x(天)之间的函数图象,根据图象回答下列问题:
如图,AB、CB表示某工厂甲、乙两车间的产量y(t)与所用时间x(天)之间的函数图象,根据图象回答下列问题: