题目内容
已知△ABC中,AB=AC=9,CD⊥AB于D,BD+BC=20,求BD和BC的长.
考点:勾股定理,等腰三角形的性质
专题:
分析:根据题意画出图形,进而利用勾股定理得出BC2-BD2=AC2-AD2,进而求出即可.
解答: 解:设BD=x,由AB=AC=9,CD⊥AB于D,BD+BC=20,则AD=9-x,BC=20-x,
解:设BD=x,由AB=AC=9,CD⊥AB于D,BD+BC=20,则AD=9-x,BC=20-x,
由题意可得:BC2-BD2=AC2-AD2,
即(20-x)2-x2=92-(9-x)2
解得:x1=50(不合题意舍去),x2=8,
则BC=20-8=12,
即BD=8,BC=12.
 解:设BD=x,由AB=AC=9,CD⊥AB于D,BD+BC=20,则AD=9-x,BC=20-x,
解:设BD=x,由AB=AC=9,CD⊥AB于D,BD+BC=20,则AD=9-x,BC=20-x,由题意可得:BC2-BD2=AC2-AD2,
即(20-x)2-x2=92-(9-x)2
解得:x1=50(不合题意舍去),x2=8,
则BC=20-8=12,
即BD=8,BC=12.
点评:此题主要考查了勾股定理以及直角三角形的性质,熟练应用勾股定理是解题关键.

练习册系列答案
相关题目
如果△ABC的∠B和∠C的角平分线交于点O,则射线AO具有如下特征的( )
| A、既平分∠BAC,又平分∠BOC |
| B、既不平分∠BAC,也不平分∠BOC |
| C、一定平分∠BAC,但不一定平分∠BOC |
| D、既不一定平分∠BAC,也不一定平分∠BOC |
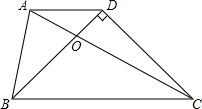 如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.
如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO. 如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则这个长方形的周长是
如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则这个长方形的周长是