题目内容
对于抛物线y=ax2+bx+c(a≠0),下列说法:
①若b2-4ac=0,则抛物线顶点一定在x轴上;
②若a>0,且一元二次方程ax2+bx+c=0有两根x1,x2(x1<x2),则ax2+bx+c<0的解集为x1<x<x2;
③若b2<3ac,则y=ax2+bx+c与x轴一定没有交点;
④若b=3a+
,则方程ax2+bx+c=0有一根为-3.
其中正确的是( )
①若b2-4ac=0,则抛物线顶点一定在x轴上;
②若a>0,且一元二次方程ax2+bx+c=0有两根x1,x2(x1<x2),则ax2+bx+c<0的解集为x1<x<x2;
③若b2<3ac,则y=ax2+bx+c与x轴一定没有交点;
④若b=3a+
| c |
| 3 |
其中正确的是( )
| A、①②③④ | B、只有①③ |
| C、只有①③④ | D、只有③④ |
考点:抛物线与x轴的交点
专题:
分析:利用抛物线与x轴的交点问题判断①正确;根据二次函数图象上点的坐标特征判断出②正确;进而利用抛物线与坐标轴交点个数确定方法以及方程根的性质求出即可.
解答:解:①若b2-4ac=0,则ax2+bx+c=0有两个相等的实数根,所以,抛物线的顶点一定在x轴上,故本小题正确;
②a>0,抛物线开口向上,ax2+bx+c<0的解集为x1<x<x2,故本小题正确;
③∵b2<3ac,∴b2-3ac<0,
∴b2-4ac<0,∴y=ax2+bx+c与x轴一定没有交点,故此选项正确;
④若b=3a+
,则9a-3b+c=0,所以方程ax2+bx+c=0有一根为-3,故此选项正确;
综上所述,正确的是①②③④.
故选:A.
②a>0,抛物线开口向上,ax2+bx+c<0的解集为x1<x<x2,故本小题正确;
③∵b2<3ac,∴b2-3ac<0,
∴b2-4ac<0,∴y=ax2+bx+c与x轴一定没有交点,故此选项正确;
④若b=3a+
| c |
| 3 |
综上所述,正确的是①②③④.
故选:A.
点评:本题考查了二次函数与不等式,二次函数图象上点的坐标特征,抛物线与x轴的交点,综合题,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
若一元二次方程ax2+bx+c=0无解,且a<0,则二次函数y=ax2+bx+c的值( )
| A、总大于0 | ||
| B、总小于0 | ||
C、在x>-
| ||
D、在x>-
|
如果△ABC的∠B和∠C的角平分线交于点O,则射线AO具有如下特征的( )
| A、既平分∠BAC,又平分∠BOC |
| B、既不平分∠BAC,也不平分∠BOC |
| C、一定平分∠BAC,但不一定平分∠BOC |
| D、既不一定平分∠BAC,也不一定平分∠BOC |
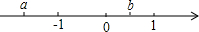 有理数a、b在数轴上对应的位置如图所示,则:①ab
有理数a、b在数轴上对应的位置如图所示,则:①ab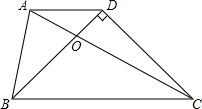 如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.
如图所示,已知AD∥BC,且BD⊥CD,BD=CD,AC=BC.求证:AB=BO.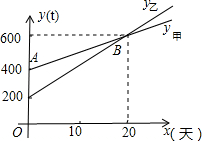 如图,AB、CB表示某工厂甲、乙两车间的产量y(t)与所用时间x(天)之间的函数图象,根据图象回答下列问题:
如图,AB、CB表示某工厂甲、乙两车间的产量y(t)与所用时间x(天)之间的函数图象,根据图象回答下列问题: