题目内容
20.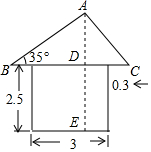 如图是某住宅区的配电房示意图(图中长度单位:m),它是一个轴对称图形,求配电房的高AE(结果精确到0.1m).
如图是某住宅区的配电房示意图(图中长度单位:m),它是一个轴对称图形,求配电房的高AE(结果精确到0.1m).(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
分析 利用轴对称的性质得到BD=0.3+1.5=1.8,再利用正切的定义得到AD=BD•tanB≈1.26,然后计算AD+DE即可.
解答 解:根据题意得BD=0.3+1.5=1.8,DE=2.5,
在Rt△ABD中,∵tanB=$\frac{AD}{BD}$,
∴AD=BD•tanB=1.8×tan35°=1.8×0.70≈1.26,
∴AE=AD+DE=1.26+2.5≈3.8(m).
答:配电房的高AE为3.8m.
点评 本题考查了解直角三角形的应用:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

练习册系列答案
相关题目
10.不等式组$\left\{\begin{array}{l}{x-5>0}\\{x+1≥0}\end{array}\right.$的解集是( )
| A. | x≥1 | B. | x>5 | C. | -1<x<5 | D. | -1≤x<5 |
8.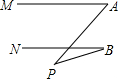 如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.
如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.
 如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.
如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
15. 实数a在数轴上的位置如图所示,则a的值可能为( )
实数a在数轴上的位置如图所示,则a的值可能为( )
 实数a在数轴上的位置如图所示,则a的值可能为( )
实数a在数轴上的位置如图所示,则a的值可能为( )| A. | -4 | B. | -3 | C. | -2 | D. | 1 |
5.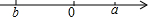 已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
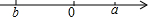 已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )| A. | a+b | B. | 3a-3b | C. | a-b | D. | a-3b |
12. 在如图所示的2017年4月份的月历表中,任意框出表中竖列上四个相邻的数,这四个数的和可能是( )
在如图所示的2017年4月份的月历表中,任意框出表中竖列上四个相邻的数,这四个数的和可能是( )
 在如图所示的2017年4月份的月历表中,任意框出表中竖列上四个相邻的数,这四个数的和可能是( )
在如图所示的2017年4月份的月历表中,任意框出表中竖列上四个相邻的数,这四个数的和可能是( )| A. | 70 | B. | 63 | C. | 99 | D. | 101 |
9.下面说法中正确的有( )
| A. | 非负数一定是正数 | |
| B. | 有最小的正整数,有最小的正有理数 | |
| C. | 0既不是整数,也不是负数 | |
| D. | 正整数和正分值统称正有理数 |
 丰县红富士苹果是江苏徐州丰县特产,某水果超市,营销员的个人收入与他每月的销售量一闪函数关系,其图象如下图所示,请你根据图象中提供的信息,解答以下问题.
丰县红富士苹果是江苏徐州丰县特产,某水果超市,营销员的个人收入与他每月的销售量一闪函数关系,其图象如下图所示,请你根据图象中提供的信息,解答以下问题.