题目内容
10. 丰县红富士苹果是江苏徐州丰县特产,某水果超市,营销员的个人收入与他每月的销售量一闪函数关系,其图象如下图所示,请你根据图象中提供的信息,解答以下问题.
丰县红富士苹果是江苏徐州丰县特产,某水果超市,营销员的个人收入与他每月的销售量一闪函数关系,其图象如下图所示,请你根据图象中提供的信息,解答以下问题.(1)求营销员的个人收入y(元)与营销员每月销售量x(千克)(x≥0)之间的函数关系式;
(2)营销员小李想得到收入1400元,她应销售多少水果?
分析 (1)根据函数图象可知y是关于x的一次函数,然后根据图象中的数据即可求得相应的函数解析式;
(2)将y=1400代入(1)中的函数解析式,即可解答本题.
解答 解:(1)设营销员的个人收入y(元)与营销员每月销售量x(千克)(x≥0)之间的函数关系式是y=kx+b,
$\left\{\begin{array}{l}{b=400}\\{4000k+b=1200}\end{array}\right.$,得$\left\{\begin{array}{l}{k=0.2}\\{b=400}\end{array}\right.$,
即营销员的个人收入y(元)与营销员每月销售量x(千克)(x≥0)之间的函数关系式是y=0.2x+400;
(2)当y=1400时,
1400=0.2x+400,
解得,x=5000,
答:她应销售5000千克的水果.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用一次函数的性质解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.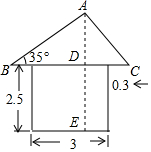 如图是某住宅区的配电房示意图(图中长度单位:m),它是一个轴对称图形,求配电房的高AE(结果精确到0.1m).
如图是某住宅区的配电房示意图(图中长度单位:m),它是一个轴对称图形,求配电房的高AE(结果精确到0.1m).
(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
 如图是某住宅区的配电房示意图(图中长度单位:m),它是一个轴对称图形,求配电房的高AE(结果精确到0.1m).
如图是某住宅区的配电房示意图(图中长度单位:m),它是一个轴对称图形,求配电房的高AE(结果精确到0.1m).(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
1.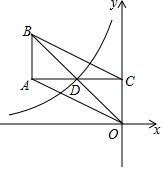 如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
 如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | 3 | D. | 6 |
5.下列运算中,正确的是( )
| A. | x3+x2=x5 | B. | x3•x2=x6 | C. | x2÷x3=x-1 | D. | (-x2)3=x6 |
2. 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )| A. | BO=OD | B. | AB=CD | C. | ∠BAD=∠BCD | D. | AC=BD |
2.$\sqrt{3}$•$\sqrt{\frac{6}{x}}$是整数,那么x是( )
| A. | 6和3 | B. | 3和1 | C. | 2和18 | D. | 只有18 |
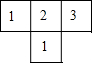 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )