题目内容
8.在还没有出现字母前,我们的祖先常用一些符号来表示方程中的未知数.现有一个方程:$\frac{2}{3}$×☆-5×☆=4,那么☆的值为$-\frac{12}{13}$.分析 设☆=x,方程变形后求出解确定出x的值,即为☆的值.
解答 解:设☆=x,方程变形为$\frac{2}{3}$x-5x=4,
去分母得:2x-15x=12,
解得:x=-$\frac{12}{13}$,
则☆的值为$-\frac{12}{13}$.
故大为;$-\frac{12}{13}$.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,∠A,∠B的平分线相交于点O,则O到AB的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
19.在下列实数中,无理数是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 0 | D. | $\frac{14}{5}$ |
20.下列方程中,有实数根的是( )
| A. | x2+x-1=0 | B. | x2+1=0 | C. | x2-x+2=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
17.函数y=$\frac{x}{\sqrt{x+2}}$中x的取值范围为( )
| A. | x≥-2且x≠0 | B. | x>-2且x≠0 | C. | x>-2 | D. | x≠0 |
18. 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )| A. | 4$\sqrt{3}$ | B. | 5$\sqrt{3}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{2}$ |
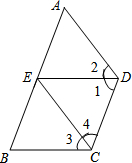 如图,AB∥DC,∠1=∠B,∠2=∠3.
如图,AB∥DC,∠1=∠B,∠2=∠3.