题目内容
10.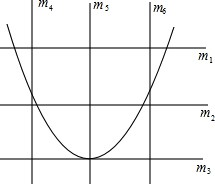 王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )| A. | m1,m4 | B. | m2,m3 | C. | m3,m6 | D. | m4,m5 |
分析 由抛物线开口向上可知a>0,将抛物线配方为y=a(x-3)2-3-9a,可得抛物线的对称轴为x=3,顶点纵坐标为-3-9a,据此结合图象可得答案.
解答 解:∵抛物线y=ax2-6ax-3的开口向上,
∴a>0,
∵y=ax2-6ax-3=a(x-3)2-3-9a,
∴抛物线的对称轴为直线x=3,
∴应选择的y轴为直线m4;
∵顶点坐标为(3,-3-9a),抛物线y=ax2-6ax-3与y轴的交点为(0,-3),而-3-9a<-3,
∴应选择的x轴为直线m1,
故选A.
点评 本题考查了二次函数的图象,理解掌握二次函数的图象与各系数的关系是解题的关键,同时注意数形结合思想的运用.

练习册系列答案
相关题目
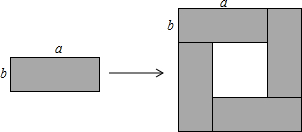
1. 如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
 如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )| A. | 4 | B. | 4a | C. | 4a+4 | D. | 2a+4 |
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,∠A,∠B的平分线相交于点O,则O到AB的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
5. 如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
 如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | 4ab=(a+b)2-(a-b)2 | D. | (a+b)(a-b)=a2-b2 |
19.在下列实数中,无理数是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 0 | D. | $\frac{14}{5}$ |
20.下列方程中,有实数根的是( )
| A. | x2+x-1=0 | B. | x2+1=0 | C. | x2-x+2=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
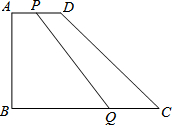 如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,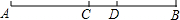 如图,点C是线段AB的中点.
如图,点C是线段AB的中点.