题目内容
19. 矩形ABCD的对角线AC、BD交于点O,∠AOD=120°,AC=4,则△ABO的周长为6.
矩形ABCD的对角线AC、BD交于点O,∠AOD=120°,AC=4,则△ABO的周长为6.
分析 由矩形的性质得出OA=OB=2,再证明△OAB是等边三角形,得出AB=OA=OB=2,即可求出△ABO的周长为.
解答 解:∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC=2,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB=2,
∵∠AOD=120°,
∴∠AOB=60°,
∴△OAB是等边三角形,
∴AB=OA=OB=2,
∴△ABO的周长=OA+OB+AB=6;
故答案为:6.
点评 本题考查了矩形的性质、等边三角形的判定与性质、三角形周长的计算;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.五一小长假期间,某景区接待游客约为630000人,将数据630000用科学记数法表示为( )
| A. | 63×103 | B. | 6.3×103 | C. | 6.3×104 | D. | 6.3×105 |
11.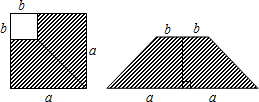 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )
在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )
 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )
在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab-b2 | D. | a2-ab=a(a-b) |
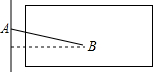 如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离大于4.6米.(填“大于”“小于”或“等于”)
如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离大于4.6米.(填“大于”“小于”或“等于”) 李老师为锻炼身体一直坚持步行上下班,一天,李老师下班后,从学校出发以45米/分的速度走了900米时,遇到一个朋友,停下来说了半小时的话,如图所示是李老师从学校到家这一过程中,距离家的路程(米)与离开学校的时间t(分)之间的关系.
李老师为锻炼身体一直坚持步行上下班,一天,李老师下班后,从学校出发以45米/分的速度走了900米时,遇到一个朋友,停下来说了半小时的话,如图所示是李老师从学校到家这一过程中,距离家的路程(米)与离开学校的时间t(分)之间的关系.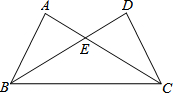 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC. 有如下问题:“如图,已知直线b、c被直线a所截,若∠1+∠2=180°,则b∥c”在你所用的方法中,推断b∥c的依据是同位角相等,两直线平行.
有如下问题:“如图,已知直线b、c被直线a所截,若∠1+∠2=180°,则b∥c”在你所用的方法中,推断b∥c的依据是同位角相等,两直线平行.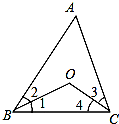 如图,BO、CO分别平分∠ABC和∠ACB.
如图,BO、CO分别平分∠ABC和∠ACB.