题目内容
15.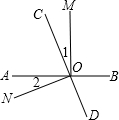 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.(1)若∠1=∠2,求∠NOD的度数;
(2)若∠1=$\frac{1}{4}$∠BOC,求∠AOC和∠BOD的度数.
分析 (1)由垂线的性质求得∠AOM=∠BOM=90°,然后根据等量代换及邻补角的定义解答;
(2)根据垂直的定义求得∠AOM=∠BOM=90°,再由∠1=$\frac{1}{4}$∠BOC求得∠BOC=120°;然后根据邻补角定义和对顶角的性质即可求解.
解答 解:(1)∵OM⊥AB,∠1=∠2,
∴∠1+∠AOC=∠2+∠AOC=90°,即∠CON=90°;
又∠NOC+∠NOD=180°,
∴∠NOD=90°;
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∵∠1=$\frac{1}{4}$∠BOC,
∴∠BOC=120°,∠1=30°;
又∠AOC+∠BOC=180°,
∴∠AOC=60°;
∴∠BOD=∠AOC=60°.
点评 本题利用垂直的定义,对顶角的性质和邻补角的定义计算,要注意领会由垂直得直角这一要点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.为了让宜兴市的山更绿、水更清,2016年市委、市政府提出了确保到2018年实现全市绿化覆盖率达到43%的目标,已知2016年绿化覆盖率为40%,设从2016年起绿化覆盖率的年平均增长率为x,则可列方程( )
| A. | 40(1+2x)=43% | B. | 40(1+2x)=43 | C. | 40(1+x)2=43 | D. | 40(1+x)2=43% |
9.蜜桔采摘开始啦!每箱蜜桔以10千克为基准,超过的千克数记为正,不足的千克数记为负,记录如图,则这4箱蜜桔的总质量是( )千克


| A. | 39.6千克 | B. | 40.4千克 | C. | 43.4千克 | D. | 40千克 |
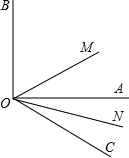 如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.
如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.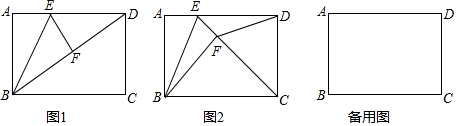
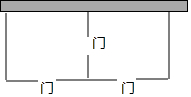 某农村拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示三处各留3m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为多少m2?
某农村拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示三处各留3m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为多少m2?