题目内容
5.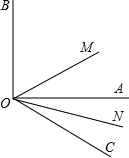 如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.
如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.
分析 根据角平分线定义求出∠NOC=$\frac{1}{2}$∠AOC,∠MOC=$\frac{1}{2}$∠BOC,根据角的和差定义得出∠MON=∠MOC-∠NOC,再代入变形即可求解.
解答  解:∵ON是∠AOC的平分线,OM是∠BOC的平分线,
解:∵ON是∠AOC的平分线,OM是∠BOC的平分线,
∴∠NOC=$\frac{1}{2}$∠AOC,∠MOC=$\frac{1}{2}$∠BOC,
∴∠MON=∠MOC-∠NOC
=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC-∠AOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°.
点评 本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠MON=$\frac{1}{2}$∠AOB.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
 如图,已知在△ABC中,AB=AC,AD∥BC,∠B=55°,则∠1=55°.
如图,已知在△ABC中,AB=AC,AD∥BC,∠B=55°,则∠1=55°.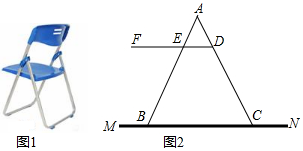
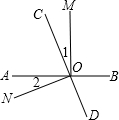 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.