题目内容
6.已知二次函数y=x2-mx+n的图象与y轴的交点到原点的距离是2.且函数图象的对称轴为x=1.求该函数解析式.分析 根据函数的对称轴公式即可求得m的值,然后根据二次函数y=x2-mx+n的图象与y轴的交点到原点的距离是2求得与y轴的交点坐标,利用待定系数法求得解析式.
解答 解:-$\frac{-m}{2}$=1,
解得:m=2,
二次函数y=x2-mx+n的图象与y轴的交点到原点的距离是2,则与y轴的交点坐标是(0,2)或(0,-2).
当与y轴的交点是(0,2)时,代入y=x2+2x+n得n=2,则函数解析式是y=x2+2x+2;
当与y轴的交点坐标是(0,-2)时,代入y=x2+2x+n,则n=-2,函数的解析式是y=x2+2x-2.
点评 本题考查了待定系数法求函数的解析式,正确理解二次函数的对称轴公式是关键.

练习册系列答案
相关题目
20.如果a2=4,|b|=2,且ab<0,则a+b的值是( )
| A. | 0 | B. | 4 | C. | ±4 | D. | 6或2 |

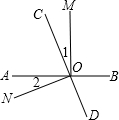 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.