题目内容
4.我们知道:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,那么$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$,$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.利用以上规律计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$.
分析 根据等式的变化可找出变化规律“$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$”,依此规律即可得出结论.
解答 解:观察,发现规律:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,
∴$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$,$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{99}$-$\frac{1}{100}$=1-$\frac{1}{100}$=$\frac{99}{100}$.
故答案为:$\frac{1}{5}$-$\frac{1}{6}$;$\frac{1}{n}$-$\frac{1}{n+1}$.
点评 本题考查了规律型中数字的变化类,根据数的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
14.若|a+1|+(b-2016)2=0,那么ab的值是( )
| A. | 1 | B. | -1 | C. | 2016 | D. | 1或-1 |
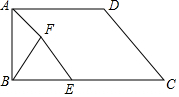 如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.
如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.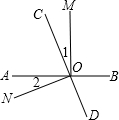 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.