题目内容
5.在⊙O中,弦AC⊥BD于点E,AC=BD.(1)如图1,求证:AB=CD;
(2)如图2,作OF⊥CD于点F,求证:AB=2OF;
(3)如图3,若AD=4,BC=8,连接OE,求OE的长.

分析 (1)由AC=BD,得到$\widehat{AC}=\widehat{BD}$,于是得到$\widehat{AB}$=$\widehat{CD}$,即可得到结论;
(2)如图2,过O作OF⊥CD于F,连接CO并延长交⊙O于G,连接BG,DG,根据圆周角定理得到∠CBG=∠CDG=90°,∠CGB=∠CDB,根据余角的性质得到∠DCE=∠BCG,得到$\widehat{BG}=\widehat{AD}$,求得$\widehat{AB}=\widehat{DG}$,得到AB=DG,推出OF∥DG,根据三角形的中位线的性质得到OF=$\frac{1}{2}$DG,等量代换得到结论;
(3)如图3,过O作OM⊥AC于M,ON⊥BD于N,根据垂径定理得到BN=DN,AM=CM,由$\widehat{AB}$=$\widehat{CD}$,得到AD∥BC,根据平行线的性质得到∠CAD=∠ACB,由圆周角定理得到∠CAD=∠DBC,等量代换得到∠ACB=∠DBC,得到△BCE是等腰直角三角形,同理△ADE是等腰直角三角形,根据勾股定理即可得到结论.
解答 解:(1)∵AC=BD,
∴$\widehat{AC}=\widehat{BD}$,
∴$\widehat{AC}-\widehat{AD}$=$\widehat{BD}$-$\widehat{AD}$,
即:$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD;
(2)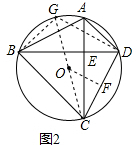 如图2,过O作OF⊥CD于F,连接CO并延长交⊙O于G,连接BG,DG,
如图2,过O作OF⊥CD于F,连接CO并延长交⊙O于G,连接BG,DG,
∴∠CBG=∠CDG=90°,∠CGB=∠CDB,
∵AC⊥BD,
∴∠CDE+∠DCE=∠BGC+∠BCG=90°,
∴∠DCE=∠BCG,
∴$\widehat{BG}=\widehat{AD}$,
∴$\widehat{AB}=\widehat{DG}$,
∴AB=DG,
∵OF⊥CD,DG⊥CD,
∴OF∥DG,
∵OC=OG,
∴CF=DF,
∴OF=$\frac{1}{2}$DG,
∴OF=$\frac{1}{2}$AB;
(3)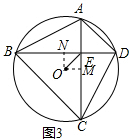 如图3,过O作OM⊥AC于M,ON⊥BD于N,
如图3,过O作OM⊥AC于M,ON⊥BD于N,
∴BN=DN,AM=CM,
∵$\widehat{AB}$=$\widehat{CD}$,
∴AD∥BC,
∴∠CAD=∠ACB,
∵∠CAD=∠DBC,
∴∠ACB=∠DBC,
∵AC⊥BD,
∴△BCE是等腰直角三角形,
同理△ADE是等腰直角三角形,
∵AD=4,BC=8,
∴AE=DE=2$\sqrt{2}$,BE=CE=4$\sqrt{2}$,
∴BD=AC=6$\sqrt{2}$,
∴BN=DN=AM=CM=3$\sqrt{2}$,
∴NE=EM=$\sqrt{2}$,
∴OE=2.
点评 本题考查了垂径定理,圆周角定理,三角形的中位线的性质,等腰直角三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | m<$\frac{9}{4}$ | B. | m>-$\frac{9}{4}$ | C. | m>$\frac{9}{4}$ | D. | m<-$\frac{9}{4}$ |
| A. | 92.59×106 | B. | 9.259×107 | C. | 9259×104 | D. | 9.259×106 |
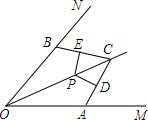 如图,OC平分∠MON,在OM、ON边上取OA=OB,点P在OC上,且PD⊥AC于D,PE⊥BC于E,求证:PD=PE.
如图,OC平分∠MON,在OM、ON边上取OA=OB,点P在OC上,且PD⊥AC于D,PE⊥BC于E,求证:PD=PE.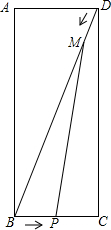 如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.
如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.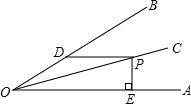 如图,∠AOB=30度,OC平分∠AOB,P为OC上一点,PD∥OA交OB于D,PE垂直OA于E,若OD=4cm,求PE的长.
如图,∠AOB=30度,OC平分∠AOB,P为OC上一点,PD∥OA交OB于D,PE垂直OA于E,若OD=4cm,求PE的长.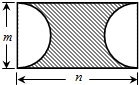 如图所示,阴影部分的面积为mn-$\frac{π{m}^{2}}{4}$(不化简也算对).
如图所示,阴影部分的面积为mn-$\frac{π{m}^{2}}{4}$(不化简也算对).