题目内容

17．若（a+3）2+$\sqrt{b-2}$=0．则点P（a，b）在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 根据非负数的性质列式求出a、b，再根据各象限内点的坐标特征解答．

解答 解：由题意得，a+3=0，b-2=0，
解得a=-3，b=2，
所以，点P的坐标为（-3，2），在第二象限．
故选B．

点评 本题考查了非负数的性质、各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．

练习册系列答案
相关题目
7．用科学记数法表示23 050 000，应记作2.305×107．
8．解方程：
（1）$\frac{1-x}{x-2}+2=\frac{1}{x-2}$
（2）$\frac{x}{x-1}$+$\frac{1}{{x}^{2}-1}$=1．
5．已知二次函数图象与直线y=$\frac{4}{3}$x+2的两个交点坐标为A（m，6）和B（-1，n）且其图象的对称轴为x=2，求它的解析式．
12．若（a-b-2）2+|a+b+3|=0，则a2-b2的值是（　　）
A．-1B．1C．6D．-6
2．已知x+y=1，
（1）用含x的代数式表示y，则y=1-x；
（2）用含y的代数式表示x，则x=1-y．
9．已知2x-y-4=0
（1）若用含x的代数式表示y，则y=2x-4；
（2）若用含y的代数式表示x，则x=$\frac{1}{2}$y+2．
6．计算
（1）|-3|-（π-1）0-（$\frac{1}{2}$）-1
（2）（-xy2）3÷（$\frac{1}{2}$xy2）2×$\frac{1}{2}$x
（3）（x-1）（x+3）+（2x-3y）（2x+3y）
（4）（2m+n）2-n（n+4m）-2m2．
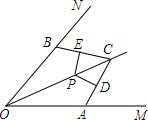16．如图，OC平分∠MON，在OM、ON边上取OA=OB，点P在OC上，且PD⊥AC于D，PE⊥BC于E，求证：PD=PE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网