题目内容
18．符合下列条件的两个三角形，不一定全等的是（ ）| A． | 底边和顶角分别相等的两个等腰三角形 | |
| B． | 有一边相等的两个等边三角形 | |
| C． | 有两边和其中一边对角对应相等的两个直角三角形 | |
| D． | 有一斜边和一直角边对应相等的两个直角三角形 |
分析 根据全等的判定方法，SSS，SAS，ASA，AAS，HL进行判断即可．
解答 解：A、底边和顶角分别相等的两个等腰三角形，符合全等的判定方法；
B、有一边相等的两个等边三角形，符合全等的判定方法；
C、有两边和其中一边对角对应相等的两个直角三角形，不符合全等的判定方法；
D、有一斜边和一直角边对应相等的两个直角三角形，符合全等的判定方法；
故选C．
点评 本题考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等，本题是一道较为简单的题目．
练习册系列答案
相关题目
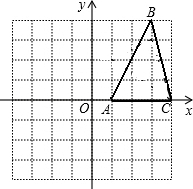如图所示，每一个小方格都是边长为1的单位正方形．△ABC的三个顶点都在格点上，以点O为坐标原点建立平面直角坐标系．
直线l是一次函数y=kx+b的图象，求出k和b的值并写出一次函数的表达式．
如图所示的直线ABC为甲地向乙地打长途电话所需付的电话费y（元）与通话时间t（min）之间的函数关系的图象．由图象可知，通话2min需付电话费1.4元，通话5min需付电话费4.4元．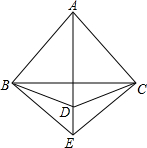
如图，AB=AC，AD平分∠BAC，求证：∠DBE=∠DCE．
8．当a＞b时，能推出$\frac{1}{a}$＞$\frac{1}{b}$，则a，b应满足条件（ ）
| A． | a＞0，b＞0 | B． | a＜0，b＜0 | C． | a＞0，b＜0 | D． | 以上答案都不对 |