题目内容
18.已知x=2-$\sqrt{3}$,求$\frac{2{x}^{2}-2}{x+1}$-$\sqrt{{x}^{2}-2x+1}$+(x+1)2的值.分析 先利用因式分解得到原式=$\frac{2(x+1)(x-1)}{x+1}$-$\sqrt{(x-1)^{2}}$+x2+2x+1,再约分和利用二次根式的性质化简得到原式=2x-2-|x-1|+x2+2x+1,然后根据x的值去绝对值后合并,最后把x的值代入计算即可.
解答 解:原式=$\frac{2(x+1)(x-1)}{x+1}$-$\sqrt{(x-1)^{2}}$+x2+2x+1
=2x-2-|x-1|+x2+2x+1,
∵x=2-$\sqrt{3}$<1,
∴原式=2x-2+x-1+x2+2x+1
=x2+5x-2
=(2-$\sqrt{3}$)2+5(2-$\sqrt{3}$)-2
=4-4$\sqrt{3}$+3+10-5$\sqrt{3}$-2
=15-9$\sqrt{3}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
8.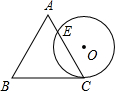 如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
 如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
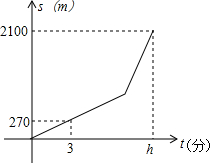 小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.
小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.