题目内容
17．
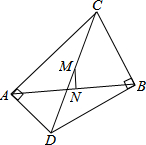如图，∠CAD和∠CBD都是直角，M是CD的中点，N是AB的中点．求证：直线MN是AB的垂直平分线．
分析 连接AM、BM，根据直角三角形斜边上的中线等于斜边的一半可得AM=BM=$\frac{1}{2}$CD，再根据等腰三角形三线合一的性质证明．
解答 
证明：如图，连接AM、BM，
∵∠CAD和∠CBD都是直角，M是CD的中点，
∴AM=BM=$\frac{1}{2}$CD，
∵N是AB的中点，
∴直线MN是AB的垂直平分线．
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记各性质并作出辅助线是解题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
如图，在四边形ABCD中，∠A=90°，AD=8．对角线BD⊥CD，P是BC边上一动点，连结PD．若∠ADB=∠C，则PD长的最小值为8．
8．
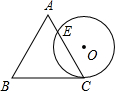如图，一个边长为a的等边三角形ABC的高与⊙O的直径相等，⊙O与BC相切于点C，⊙O与AC相交于点E，则AE：EC的值为（ ）
如图，一个边长为a的等边三角形ABC的高与⊙O的直径相等，⊙O与BC相切于点C，⊙O与AC相交于点E，则AE：EC的值为（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
