题目内容
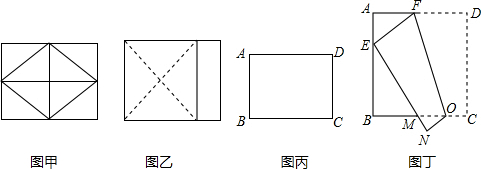
12. 如图,在四边形ABCD中,M,N,E,F分别为AD,BC,BD,AC的中点,求证:MN与EF互相平分.
如图,在四边形ABCD中,M,N,E,F分别为AD,BC,BD,AC的中点,求证:MN与EF互相平分.
分析 连接ME、EN、NF、MF,根据三角形的中位线平行于第三边并且等于第三边的一半可得ME∥AB且ME=$\frac{1}{2}$AB,NF∥AB且NF=$\frac{1}{2}$AB,然后求出ME∥NF且ME=NF,再根据一组对边平行且相等四边形是平行四边形求出四边形MENF是平行四边形,然后根据平行四边形对角线互相平分证明即可.
解答  证明:如图,连接ME、EN、NF、MF,
证明:如图,连接ME、EN、NF、MF,
∵M,N,E,F分别为AD,BC,BD,AC的中点,
∴ME∥AB且ME=$\frac{1}{2}$AB,NF∥AB且NF=$\frac{1}{2}$AB,
∴ME∥NF且ME=NF,
∴四边形MENF是平行四边形,
∴MN与EF互相平分.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定与性质,熟记定理并作辅助线构造出以MN、EF为对角线的平行四边形是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
17.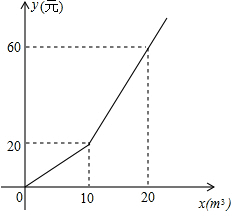 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
(1)设某用户月用水量为xm3,交水费y元,求a的值及y与x的函数关系式
(2)若该户居民三、四月份共用水20m3,且四月份用水量超过三月份,共交水费52元,则该户居民三、四月份各用水多少立米?
 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.| 每月用水量 (m3) | 单价(元/m3) |
| 不超出10m3的部分 | a |
| 超出10m3的部分 | a+2 |
(2)若该户居民三、四月份共用水20m3,且四月份用水量超过三月份,共交水费52元,则该户居民三、四月份各用水多少立米?
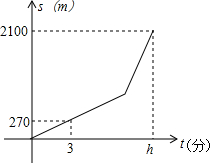 小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.
小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.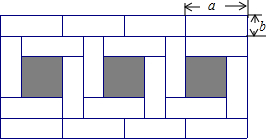 已知将同样大小的小长方形纸片拼成的如图形状的大长方形(小长方形纸片长为a,宽为b)请你仔细观察图形,解答下列问题:
已知将同样大小的小长方形纸片拼成的如图形状的大长方形(小长方形纸片长为a,宽为b)请你仔细观察图形,解答下列问题: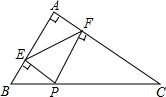 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.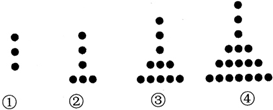
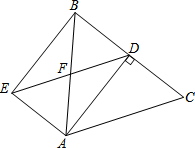 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.