题目内容
17.如果|x|+y2=5,且y=-1,则x=±4.分析 根据|x|+y2=5,且y=-1,可以求得x的值,本体得以解决.
解答 解:∵|x|+y2=5,且y=-1,
∴|x|+(-1)2=5,
即|x|+1=5,
解得,x=±4,
故答案为:±4.
点评 本题考查有理数的乘方、绝对值、有理数的加法,解题的关键是明确它们各自的计算方法,尤其是明确绝对值相等的数有两个,它们互为相反数.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
5.两条平行线被第三条直线所截,一对同旁内角的比为2:7,则这两个角中较大的角的度数为( )
| A. | 40° | B. | 70° | C. | 100° | D. | 140° |
2.若a>1,在下面四组数中,能组成直角三角形的是( )
| A. | a-1、a+1、$\sqrt{1+{a}^{2}}$ | B. | 3(a-1)、4(a-1)、5(a-1) | C. | a-1、a、a+1 | D. | a+2、a、$\sqrt{2{a}^{2}+4}$ |
9.若代数式$\sqrt{2-x}+\sqrt{3x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥2 | B. | x≤$\frac{2}{3}$ | C. | $\frac{2}{3}≤x≤2$ | D. | $\frac{2}{3}<x<2$ |
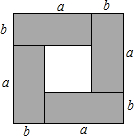 利用图形的面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
利用图形的面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.