题目内容
5.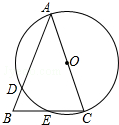 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;
(2)若∠B=70°,求弧DE的度数.
(3)若BD=2,BE=3,求AC的长.
分析 (1)连结AE,如图,由圆周角定理得∠AEC=90°,而AB=AC,则根据等腰三角形的性质即可判断BE=CE;
(2)连结OD、OE,如图,在Rt△ABE中,利用互余计算出∠BAE=20°,再根据圆周角定理得∠DOE=2∠DAE=40°,然后根据圆心角的度数等于它所对的弧的度数即可得到弧DE的度数为40°;
(3)连结CD,如图,BC=2BE=6,设AC=x,则AD=x-2,由圆周角定理得∠ADC=90°,在Rt△BCD中,利用勾股定理得CD2=32,然后在Rt△ADC中再利用勾股定理得到(x-2)2+32=x2,接着解方程求出x即可.
解答 (1)证明:连结AE,如图,
∵AC为直径,
∴∠AEC=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE;
(2)解:连结OD、OE,如图,
在Rt△ABE中,∠BAE=90°-∠B=90°-70°=20°,
∴∠DOE=2∠DAE=40°,
∴弧DE的度数为40°;
(3)解:连结CD,如图,BC=2BE=6,设AC=x,则AD=x-2,
∵AC为直径,
∴∠ADC=90°,
在Rt△BCD中,CD2=BC2-BD2=62-22=32,
在Rt△ADC中,∵AD2+CD2=AC2,
∴(x-2)2+32=x2,解得x=9,
即AC的长为9.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质.

练习册系列答案
相关题目
14.若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2015-a-b的值是( )
| A. | 2017 | B. | 2018 | C. | 2019 | D. | 2020 |
14.下列式子中错误的是( )
| A. | -0.3>-$\frac{1}{3}$ | B. | (-2)2<(-2)3 | C. | (-2)2>-32 | D. | -$\frac{9}{10}$<-$\frac{8}{9}$ |
15.在下列条件中,不能作为判断△ABC≌△DEF的条件是( )
| A. | AB=DE,AC=DF,∠A=∠D | B. | ∠A=∠D,∠B=∠E,AC=DF | ||
| C. | AB=DE,BC=EF,∠C=∠F | D. | AB=DE,AC=DF,BC=EF |
 是关于
是关于 的一元一次方程,则
的一元一次方程,则 的值为_____________
的值为_____________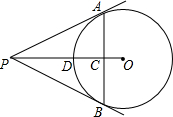 如图,PA、PB切⊙O于点A、B,PO与AB交于点C,PO交⊙O于点D,且PA=8,PO=10,则OC=$\frac{18}{5}$.
如图,PA、PB切⊙O于点A、B,PO与AB交于点C,PO交⊙O于点D,且PA=8,PO=10,则OC=$\frac{18}{5}$.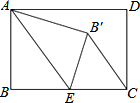 如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C
如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C