题目内容
19.某商场销售一种进价为每箱40元的纯牛奶,销售过程中发现,若每箱以55元出售,每天可售出75箱,且每箱涨价1元,则每天可少销售3箱.(1)球出去每天销售y(件)与销售单价x(元)之间的函数关系式;
(2)若该商场每天销售这种纯牛奶获得的利润为W元.试求出利润W(元)与销售单价x(元)之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
分析 (1)根据每天的销量=原来的销量-每天减少的销量就可以得出售量y与销售单价x之间的函数关系式;
(2)销售利润w(元)=每箱的销售利润×每天的销售量,根据题中所给的自变量的取值得到二次的最值问题即可.
解答 解:(1)y=75-3(x-55)=-3x+240;
(2)W=(x-40)(-3x+240)
=-3x2+360x-9600,
∵-3<0
∴抛物线开口向下.
当x=-$\frac{b}{2a}$=60时,y有最大值.
y最大=$\frac{4ac-{b}^{2}}{4a}$=1200
∴当售价为60元时,y的最大值为1200元.
∴当每箱纯牛奶的销售价为60元时,可以获得1200元的最大利润.
点评 此题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常用函数的增减性来解答,要注意应该在自变量的取值范围内求最大值(或最小值).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B.  C.
C.  D.
D. 
 如图,正方形ABCD的边长为5,以A为原点,AB所在的直线为x轴建立平面直角坐标系,在图中画出y轴,并写出A、B、C、D四个顶点的坐标.
如图,正方形ABCD的边长为5,以A为原点,AB所在的直线为x轴建立平面直角坐标系,在图中画出y轴,并写出A、B、C、D四个顶点的坐标.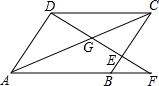 如图,在平行四边形ABCD中,点E在边BC上,DE的延长线交AB的延长线于点F,AC与DF交于G,BE:AD=1:3
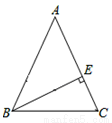
如图,在平行四边形ABCD中,点E在边BC上,DE的延长线交AB的延长线于点F,AC与DF交于G,BE:AD=1:3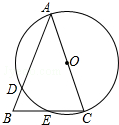 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.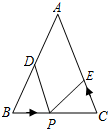 如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.